题目内容
设函数 是
是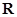 上以4为周期的可导偶函数,则曲线
上以4为周期的可导偶函数,则曲线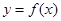 在
在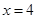 处的切线的斜率为()
处的切线的斜率为()
A.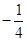 | B. | C. | D.4 |
B
解析试题分析:∵f(x)是R上可导偶函数,∴f(x)的图象关于y轴对称,∴f(x)在x=0处取得极值,即 ,又∵f(x)的周期为5,∴f′(5)=0,即曲线y=f(x)在x=5处的切线的斜率0,故选项为B.
,又∵f(x)的周期为5,∴f′(5)=0,即曲线y=f(x)在x=5处的切线的斜率0,故选项为B.
考点:1.函数在某点取得极值的条件;2.函数奇偶性的性质;3.三角函数的周期性及其求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(5分)(2011•天津)对实数a与b,定义新运算“?”:a?b= .设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
.设函数f(x)=(x2﹣2)?(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
| A.(﹣1,1]∪(2,+∞) | B.(﹣2,﹣1]∪(1,2] | C.(﹣∞,﹣2)∪(1,2] | D.[﹣2,﹣1] |
函数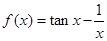 在区间
在区间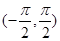 内的零点个数是( )
内的零点个数是( )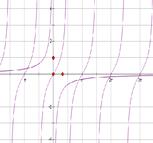
| A.0 | B.1 | C.2 | D.3 |
下列函数中,既是偶函数又在区间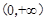 上单调递增的是( )
上单调递增的是( )
A.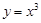 | B.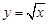 | C.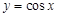 | D.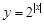 |
(2013•重庆)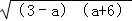 (﹣6≤a≤3)的最大值为( )
(﹣6≤a≤3)的最大值为( )
| A.9 | B.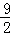 | C.3 | D.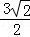 |
(2011•山东)曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是( )
| A.﹣9 | B.﹣3 | C.9 | D.15 |
下列函数中与函数y=-3|x|奇偶性相同且在(-∞,0)上单调性也相同的是( )
A.y=- | B.y=log2|x| |
| C.y=1-x2 | D.y=x3-1 |
若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是( )
| A.(-2,2) | B.[-2,2] | C.(-1,1) | D.[-1,1] |
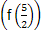 的值是( )
的值是( )
