题目内容
如右图已知每条棱长都为3的四棱柱ABCD-A B
B C
C D
D 中,底面是菱形,
中,底面是菱形, BAD=60°,D B
BAD=60°,D B ⊥平面ABCD,长为2的线段MN的一个端点M在DD
⊥平面ABCD,长为2的线段MN的一个端点M在DD 上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与此四棱柱的面所围成的几何体的体积为 _____________
上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与此四棱柱的面所围成的几何体的体积为 _____________

解析试题分析:
取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
以DE所在直线为x轴,以DC所在直线为y轴,以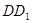 所在直线为z轴建立如图空间直角坐标系
所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P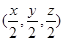 ,
,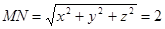
∴
∴
∴
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的 ,
,
∴几何体的体积为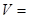
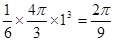
考点:棱柱、棱锥、棱台的体积;棱柱的结构特征.
点评:本题考查几何体的体积,须先用代数法确定点的轨迹,然后熟练应用体积公式即可,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 且
且 .给出下列命题:
.给出下列命题: 且
且 ;
; 
 中,
中, 两两垂直,且
两两垂直,且 .设点
.设点 为底面
为底面 内一点,定义
内一点,定义 ,其中
,其中 分别为三棱锥
分别为三棱锥 、
、 、
、 的体积.若
的体积.若 ,且
,且 恒成立,则正实数
恒成立,则正实数 的取值范围是___________.
的取值范围是___________.
 、
、 是直线,
是直线, 、
、 是平面,
是平面, ,向量
,向量 在
在 在
在 ,
,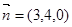 ,则
,则 ∥
∥ ;
; 和直线
和直线 ,给出下列条件:①
,给出下列条件:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .则使
.则使 成立的充分条件是 .(填序号)
成立的充分条件是 .(填序号) 是两个不同的平面,
是两个不同的平面, 是两条不同直线.①若
是两条不同直线.①若 ,则
,则
 ,则
,则
 ,则
,则
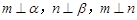 ,则
,则 以上命题正确的是 .(将正确命题的序号全部填上)
以上命题正确的是 .(将正确命题的序号全部填上)