题目内容
(本题满分13分)已知函数f(x)=2x2-2ax+b,f(-1)=-8.对![]() x∈R,都有f(x)≥f(-1)成立;记集合A={ x | f(x)>0},B={ x | | x-t |≤1 }.(1) 当t=1时,求(
x∈R,都有f(x)≥f(-1)成立;记集合A={ x | f(x)>0},B={ x | | x-t |≤1 }.(1) 当t=1时,求(![]() RA)∪B;(2) 设命题P:A∩B≠
RA)∪B;(2) 设命题P:A∩B≠![]() ,若┐P为真命题,求实数t的取值范围.
,若┐P为真命题,求实数t的取值范围.
(Ⅰ) { x | -3≤x≤2}. (Ⅱ) [-2, 0]
解析:
由题意(-1, -8)为二次函数的顶点,∴ f(x)=2(x+1)2-8=2(x2+2x-3).
A={ x | x<-3或x>1}.
??????(1) B={ x | |x-1|≤1}={ x | 0≤x≤2}.
∴ ( ![]() RA)∪B={ x | -3≤x≤1}∪{ x | 0≤x≤2}={ x | -3≤x≤2}.
RA)∪B={ x | -3≤x≤1}∪{ x | 0≤x≤2}={ x | -3≤x≤2}.
??????(2) B={ x | t-1≤x≤t+1}. ![]() ,∴实数t的取值范围是[-2, 0].
,∴实数t的取值范围是[-2, 0].

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.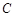 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.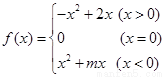 为奇函数;
为奇函数;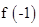 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆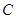 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.