题目内容
已知正态分布N(μ,σ2)的密度曲线是f(x)=| 1 | ||
|
| (x-μ)2 |
| 2σ2 |
①对任意x∈R,f(μ+x)=f(μ-x)成立;
②如果随机变量ξ服从N(μ,σ2),且F(x)=P(ξ<x),那么F(x)是R上的增函数;
③如果随机变量ξ服从N(108,100),那么ξ的期望是108,标准差是100;
④随机变量ξ服从N(μ,σ2),P(ξ<1)=
| 1 |
| 2 |
分析:作出正态分布N(μ,σ2)的密度曲线是:由图分析可得4个命题的正确与否,进而可得答案.
解答: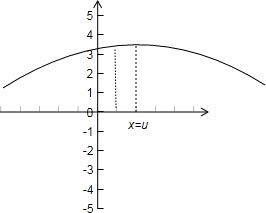 解:画出正态分布N(μ,σ2)的密度曲线如下图:
解:画出正态分布N(μ,σ2)的密度曲线如下图:
由图可得:
①图象关于x=μ对称;故①正确;
②随着x的增加,F(x)=P(ξ<x)也随着增加;故②正确;
③如果随机变量ξ服从N(108,100),那么ξ的期望是108,标准差是10;
④由图象的对称性,可得④正确.
故填:①②④.
 解:画出正态分布N(μ,σ2)的密度曲线如下图:
解:画出正态分布N(μ,σ2)的密度曲线如下图:由图可得:
①图象关于x=μ对称;故①正确;
②随着x的增加,F(x)=P(ξ<x)也随着增加;故②正确;
③如果随机变量ξ服从N(108,100),那么ξ的期望是108,标准差是10;
④由图象的对称性,可得④正确.
故填:①②④.
点评:本题考查正态分布的图象与性质,学习正态分布,一定要紧紧抓住平均数μ和标准差σ这两个关键量;3.结合正态曲线的图形特征,归纳正态曲线的性质.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
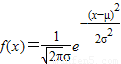 ,给出以下四个命题:
,给出以下四个命题: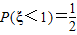 ,P(ξ>2)=p,则P(0<ξ<2)=1-2p;其中,真命题的序号是 .(写出所有真命题序号)
,P(ξ>2)=p,则P(0<ξ<2)=1-2p;其中,真命题的序号是 .(写出所有真命题序号)