Question

(1)求经过点P(3，2)和Q(-6，7)的双曲线的标准方程；

 (2)已知双曲线与椭圆=1有相同的焦点，且与椭圆的一个交点的纵坐标为4，求双曲线的标准方程.

Answer 1

解析：(1)可设所求双曲线的方程为Ax²+By²=1(AB＜0).

∵双曲线经过(3，27)和(-62，7)点

∴

解得A=-，B=

故所求双曲线方程为：=1.

(2)椭圆的焦点为F₁(0，-3)，F₂(0，3)，故可设双曲线方程为=1(a＞0,b＞0)且c=3,a²+b²=9.

根据条件知，双曲线与椭圆的一个交点的纵坐标为4，可得其y轴正半轴两交点的坐标为A(，4)、B(-，4)，由交点A在双曲线上，则=1.解方程组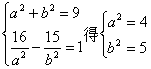

故所求双曲线方程=1