题目内容
求由下列条件所决定圆x2+y2=4的圆的切线方程:(1)经过点P(
| 3, |
分析:(1)当切线斜率不存在时,直线与圆位置关系是相交,不合题意,所以设切线方程的斜率为k,根据P的坐标写出切线的方程,然后根据直线与圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到直线的距离d,让d等于半径r列出关于k的方程,求出方程的解即可得到k的值,根据求出的k的值和P的坐标写出切线方程即可;
(2)当切线斜率不存在时,直线与圆位置关系是外离,不合题意,所以设出切线方程的斜率为k,根据直线与圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到直线的距离d,让d等于圆的半径r列出关于k的方程,求出方程的解即可得到k的值,由k的值和Q的坐标写出切线方程即可;
(3)设出切点的坐标为(a,b),根据已知的斜率为-1,表示出切线的方程,然后利用点到直线的距离公式表示出圆心到所设直线的距离d,让d等于圆的半径r列出关于a与b的绝对值关系式,经讨论得到关于a与b的两关系式,分别记作①和②,把切点的坐标代入圆的方程,得到关于a与b的关系式,记作③,把①③联立,②③联立,分别求出两对a与b的值,得到切点的坐标有两个,根据求出的切点坐标和已知的切线的斜率写出切线方程即可.
(2)当切线斜率不存在时,直线与圆位置关系是外离,不合题意,所以设出切线方程的斜率为k,根据直线与圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到直线的距离d,让d等于圆的半径r列出关于k的方程,求出方程的解即可得到k的值,由k的值和Q的坐标写出切线方程即可;
(3)设出切点的坐标为(a,b),根据已知的斜率为-1,表示出切线的方程,然后利用点到直线的距离公式表示出圆心到所设直线的距离d,让d等于圆的半径r列出关于a与b的绝对值关系式,经讨论得到关于a与b的两关系式,分别记作①和②,把切点的坐标代入圆的方程,得到关于a与b的关系式,记作③,把①③联立,②③联立,分别求出两对a与b的值,得到切点的坐标有两个,根据求出的切点坐标和已知的切线的斜率写出切线方程即可.
解答:解:(1)经判断,得到点P在圆上,
当斜率k不存在时,直线与圆相交,不合题意,所以设切线方程的斜率为k,
则切线方程为:y-1=k(x-
),
所以圆心(0,0)到直线的距离d=
=r=2,
化简得:(k+
)2=0,解得k=-
,
所以切线方程为:y=-
x+4;
(2)当直线斜率不存在时,直线与圆外离,不合题意,设过点Q的切线方程的斜率为k,
则切线方程为y=k(x-3),
所以圆心到直线的距离d=
=r=2,
化简得:k=±
,
所以切线方程为:y=
x-
或y=-
x+
;
(3)设切点坐标为(a,b),则切线方程为:y-a=-(x-b),即x+y-a-b=0,
所以圆心到直线的距离d=
=2,即a+b=2
①或a+b=-2
②,
又把切点坐标代入圆的方程得:a2+b2=4③,
由①得:a=2
-b,代入③得:a=b=
;由②得:a=-2
-b,代入③得:a=b=-
,
所以切点坐标分别为(
,
)或(-
,-
),
则切线方程为:y-
=-(x-
)或y+
=-(x+
),
即x+y-2
=0或x+y+2
=0.
当斜率k不存在时,直线与圆相交,不合题意,所以设切线方程的斜率为k,
则切线方程为:y-1=k(x-
| 3 |
所以圆心(0,0)到直线的距离d=
|1-
| ||
|
化简得:(k+
| 3 |
| 3 |
所以切线方程为:y=-
| 3 |
(2)当直线斜率不存在时,直线与圆外离,不合题意,设过点Q的切线方程的斜率为k,
则切线方程为y=k(x-3),
所以圆心到直线的距离d=
| |-3k| | ||
|
化简得:k=±
2
| ||
| 5 |
所以切线方程为:y=
2
| ||
| 5 |
6
| ||
| 5 |
2
| ||
| 5 |
6
| ||
| 5 |
(3)设切点坐标为(a,b),则切线方程为:y-a=-(x-b),即x+y-a-b=0,
所以圆心到直线的距离d=
| |a+b| | ||
|
| 2 |
| 2 |
又把切点坐标代入圆的方程得:a2+b2=4③,
由①得:a=2
| 2 |
| 2 |
| 2 |
| 2 |
所以切点坐标分别为(
| 2 |
| 2 |
| 2 |
| 2 |
则切线方程为:y-
| 2 |
| 2 |
| 2 |
| 2 |
即x+y-2
| 2 |
| 2 |
点评:此题考查学生掌握直线与圆相切时圆心到直线的距离等于圆的半径,灵活运用点到直线的距离公式化简求值,是一道中档题.

练习册系列答案
相关题目
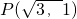 ,(2)经过点Q(3,0),(3)斜率为-1.
,(2)经过点Q(3,0),(3)斜率为-1.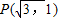 ,(2)经过点Q(3,0),(3)斜率为-1.
,(2)经过点Q(3,0),(3)斜率为-1.