题目内容
已知f(x)=ax3-2ax2+b,(a≠0).(Ⅰ)求出f(x)的极值点,并指出其是极大值点还是极小值点;
(Ⅱ)若f(x)在区间[-2,1]上最大值是5,最小值是-11,求f(x)的解析式.
分析:(1)分类讨论参数a,满足f′(x)=0的点附近的导数的符号的变化情况,来确定极值点,从而求出极值;
(2)先求出f(x)在区间[-2,1]的极值,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值,建立两个等量关系,求出参数a,b即可.
(2)先求出f(x)在区间[-2,1]的极值,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值,建立两个等量关系,求出参数a,b即可.
解答:解(Ⅰ)∵f(x)=ax3-2ax2+b,
∴f′(x)=3ax2-4ax=ax(3x-4)
令f′(x)=0,得x1=0,x2=
ia<0时
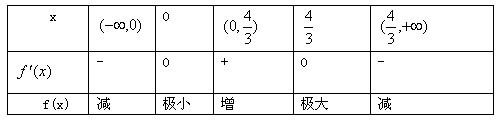
函数的极值点是0,
,0是极小值点,
是极大值点(5分)
ii、a>0时
同理可以验证0是极大值点,
是极小值点(6分)
(Ⅱ)f(x)在区间[-2,1]上最大值是5,
最小值是-11,f′(x)=0,x1=0,x2=
∉[-2,1]
若a>0,
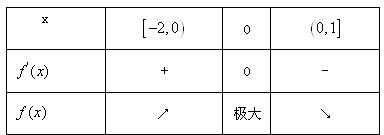 (8分)
(8分)
因此f(0)必为最大值,∴f(0)=5,得b=5,
∵f(-2)=-16a+5,f(1)=-a+5,∴f(1)>f(-2)
∴f(-2)=-16a+5=-11,∴a=1
∴f(x)=x3-2x2+5;(11分)
若a<0,同理可得f(0)为最小值,∴f(0)=-11,得b=-11,
∵f(-2)=-16a+5,f(1)=-a+5,∴f(-2)>f(1)
∴f(-2)=f(x)max=5,∴a=-1∴f(x)=-x3+2x2-11.(14分)
∴f′(x)=3ax2-4ax=ax(3x-4)
令f′(x)=0,得x1=0,x2=
| 4 |
| 3 |
ia<0时

函数的极值点是0,
| 4 |
| 3 |
| 4 |
| 3 |
ii、a>0时
同理可以验证0是极大值点,
| 4 |
| 3 |
(Ⅱ)f(x)在区间[-2,1]上最大值是5,
最小值是-11,f′(x)=0,x1=0,x2=
| 4 |
| 3 |
若a>0,
 (8分)
(8分)因此f(0)必为最大值,∴f(0)=5,得b=5,
∵f(-2)=-16a+5,f(1)=-a+5,∴f(1)>f(-2)
∴f(-2)=-16a+5=-11,∴a=1
∴f(x)=x3-2x2+5;(11分)
若a<0,同理可得f(0)为最小值,∴f(0)=-11,得b=-11,
∵f(-2)=-16a+5,f(1)=-a+5,∴f(-2)>f(1)
∴f(-2)=f(x)max=5,∴a=-1∴f(x)=-x3+2x2-11.(14分)
点评:本题主要考查了利用导数研究函数的极值,以及待定系数法求函数解析式和利用导数求闭区间上函数的最值,属于中档题.

练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |