题目内容
关于x、y的二元线性方程组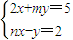
的增广矩阵经过变换，最后得到的矩阵为
，则二阶行列式
= ．
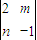【答案】分析：先由矩阵为 
，对应的方程为：
，再由题意得：关于x、y的二元线性方程组的解为：
，从而求得m，n的值，最后利用行列式的计算法则求解即可．
解答：解：矩阵为
，对应的方程组为：
，
由题意得：关于x、y的二元线性方程组
的解为：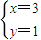
，
∴
⇒
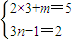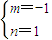
∴则二阶行列式
=-2-mn=-1
故答案为：-1．
点评：本题主要考查了几种特殊的矩阵变换，解答的关键是对增广矩阵的理解，利用方程组同解解决问题．
，对应的方程为：，再由题意得：关于x、y的二元线性方程组的解为：，从而求得m，n的值，最后利用行列式的计算法则求解即可．解答：解：矩阵为
，对应的方程组为：，由题意得：关于x、y的二元线性方程组
的解为：，∴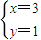
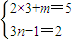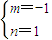
⇒∴则二阶行列式
=-2-mn=-1故答案为：-1．
点评：本题主要考查了几种特殊的矩阵变换，解答的关键是对增广矩阵的理解，利用方程组同解解决问题．
练习册系列答案
相关题目
关于x、y的二元线性方程组
，的增广矩阵经过变换，最后得到的矩阵为
，则 m+n=（ ）
|
|
|
| A、-1 | ||
B、
| ||
C、
| ||
D、-
|