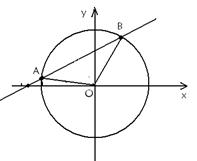
题目内容

已知直线y=
3
-x与圆x2+y2=2相交于A，B两点，是优弧AB上任意一点，则∠APB=（　　）
A、
2π
3
B、
π
6
C、
5π
6
D、
π
3
分析：先求圆心到直线的距离，从而求出AB所对的圆心角，进而求出∠APB．
解答：解：圆心到直线的距离d=
3
2
=
6
2
，AB=2
2-
3
2
=
2
=半径所以AB所对的圆心角是60°，
所对的圆周角是30°，即∠APB=30°，
选B．
点评：本题主要考查直线与圆相交问题，利用圆心到直线的距离求解时关键．
练习册系列答案
相关题目
已知直线y=-2x-
2
3
与曲线f(x)=
1
3
x3-bx相切．
（1）求b的值
（2）若方程f（x）=x2+m在（0，+∞）上有两个解x1，x2．
求：①m的取值范围     ②比较x1x2+9与3（x1+x2）的大小．
已知直线y=
3
(x-2)与抛物线C：y2=8x相交于A、B两点，F为C的焦点，若
AF
=λ
FB
，（|
AF
|＞|
FB
|），则λ=（　　）
已知抛物线C的顶点在原点，焦点为F(
1
2
，0)．（1）求抛物线C的方程； （2）已知直线y=k(x+
1
2
) 与抛物线C交于A、B 两点，且|FA|=2|FB|，求k 的值； （3）设点P 是抛物线C上的动点，点R、N 在y 轴上，圆（x-1）2+y2=1 内切于△PRN，求△PRN 的面积最小值．

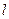（本小题满分14分）已知直线:y=k(x+2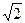)与圆O：x2+y2=4相交于不重合的
A、B两点，O是坐标原点，且三点A、B、O构成三角形．
（1）求k的取值范围；
（2）三角形ABO的面积为S，试将S表示成k的函数，并求出它的定义域；
（3）求S的最大值，并求取得最大值时k的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网