Question

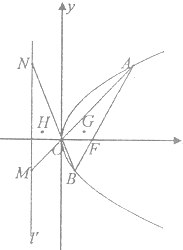
过点F（1，0）的直线l交抛物线C：y²=4x于A，B两点．
（1）若|AB|=8，求直线l的方程；
（2）记抛物线C的准线为l，设OA，OB分别交l于M，N两点，△AOB与△MON的重心分别为G，H，求|GH|的最小值．

Answer 1

分析：设A（x₁，y₁），B（x₂，y₂），直线l的方程为x=ky+1，代入抛物线方程，根据方程的根与系数关系y₁+y₂，x₁+x₂=k（y₁+y₂）+2
（1）|AB|=x1+

1

2

p + x2+

1

2

p=8，代入可求k，进而可求直线方程
（2）由重心坐标公式可得，

x0= x1+x2 3 = 2+4k2 3 y0= y1+y2 3 = 4k 3

可求G
由直线OA的方程y=

y1

x1

x，与准线相交得M（-1，-

-y1

x1

）；直线OB的方程y=

y2

x2

x，与准线相交得N（-1，-

y2

x2

），从而可求H，而|GH|=x_G-x_H，利用二次函数的性质可求

解答：解：设直线l的方程为x=ky+1，代入C：y²=4x可得y²-4ky-4=0
设A（x₁，y₁），B（x₂，y₂）
则y₁+y₂=4k，x₁+x₂=k（y₁+y₂）+2=4k²+2
（1）|AB|=x1+

1

2

p + x2+

1

2

p=4k²+2+2=8
∴k=±1
故直线l的方程为x±y-1=0
（2）由重心坐标公式可得，

x0= x1+x2 3 = 2+4k2 3 y0= y1+y2 3 = 4k 3

∴G（

2+4k2

3

，

4k

3

）
直线OA的方程y=

y1

x1

x，与准线相交得M（-1，-

-y1

x1

）
直线OB的方程y=

y2

x2

x，与准线相交得N（-1，-

y2

x2

）
∴xH=-

2

3

，yH=-

1

3

(

y1

x1

+

y2

x2

)=-

1

3

•

2ky1y2 +(y1+y2)

x1x2

=

4k

3

，故H（-

2

3

，

4k

3

）
|GH|=x_G-x_H=

1

3

(4k2+4)≥

4

3

即|GH|的最小值

4

3

点评：本题主要考察了利用抛物线的定义求解抛物线的焦点弦，主要利用了焦半径公式，三角形的重心坐标公式的应用是解答本题的关键