题目内容
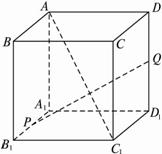
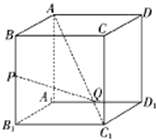 如图,AC1是正方体的一条对角线,点P、Q分别为其所在棱的中点,则异面直线PQ与AC1所成的角为________.
如图,AC1是正方体的一条对角线,点P、Q分别为其所在棱的中点,则异面直线PQ与AC1所成的角为________.

分析:取AB1的中点R,连接PR,QR,BD,AB,AD,在正方体中,根据线面垂直的判定定理可得线面垂直:AC1⊥平面ABD,再根据面面平行的判定定理可得面面平行.结合线面垂直的判定定理得出AC1⊥平面PQR,最后利用线面垂直的性质定理得出PQ⊥AC1.从而异面直线PQ与AC1所成的角直角.
解答:
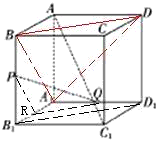 解:取AB1的中点R,连接PR,QR,BD,AB,AD,
解:取AB1的中点R,连接PR,QR,BD,AB,AD,在正方形ABCD中,BD⊥AC,BD⊥CC1,
∴BD⊥平面AC1
从而得到BD⊥AC1,
同理得AB⊥AC1,
∴AC1⊥平面ABD,
因为P,Q,R分别是棱BB1,AD1,AB1的中点,
所以PR∥AB,
所以QR∥B1D1∥BD,
∴平面PQR∥平面ABD,
∴AC1⊥平面PQR,
又因为PQ?平面PQR,
所以PQ⊥AC1.
则异面直线PQ与AC1所成的角为
 .
.故答案为:
 .
.点评:本题主要考查线面平行、线面垂直的判定定理,以及解决异面直线及其所成的角的问题.属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
如图,P是正方体ABCD-A1B1C1D1对角线AC1上一动点,设AP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( ) (2010•孝感模拟)如图,AC1是正方体的一条对角线,点P、Q分别为其所在棱的中点,则异面直线PQ与AC1所成的角为
(2010•孝感模拟)如图,AC1是正方体的一条对角线,点P、Q分别为其所在棱的中点,则异面直线PQ与AC1所成的角为