题目内容
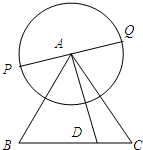如图△ABC为正三角形，边长为2，以点A为圆心，1为半径作圆，PQ为圆A的任意一条直径．（1）若
| CD |
| 1 |
| 3 |
| DB |
| AD |
（2）求
| BP |
| CQ |
（3）判断B
| P |
| Q |
| P |
| B |
分析：（1′）利用向量加法的三角形法则，将向量
表示成：
=
+
，再结合向量的模的性质求出它的模即可；
（2）先结合图形利用平面向量基本定理将向量
，
分别用向量
+
和
+
表示，再利用题中条件化成1+2cosθ，最后结合三角函数的性质求
•
的最大值．
（3）将B
•C
-A
•C
利用平面向量基本定理化简成：-|A
|2+A
•A
，再结合向量的数量积公式即可得出不会随点P的变化而变化，值为1．
| AD |
| AD |
| AC |
| 1 |
| 4 |
| CB |
（2）先结合图形利用平面向量基本定理将向量
| BP |
| CQ |
| BA |
| AP |
| CA |
| AQ |
| BP |
| CQ |
（3）将B
| P |
| Q |
| P |
| B |
| P |
| B |
| C |
解答：解：（1）∵
=
+
，
∴|
|=
=
=
；
（2）
（其中θ为
与
的夹角）所以 θ=0时，(
•
)取最大值3．
（3）由于B
•C
-A
•C
=(A
-A
)•(A
-A
)-A
(A
-A
)，A
=-A
B
•C
-A
•C
=(A
-A
)•(-A
-A
)-A
(A
-A
)=-|A
|2+A
•A
．因为A
•A
=|A
|•|A
|cos∠BAC=2，|A
|2=1，
所以B
•C
-A
•C
=-|A
|2+A
•A
=1，即B
•C
-A
•C
不会随点P的变化而变化，值为1．
| AD |
| AC |
| 1 |
| 4 |
| CB |
∴|
| AD |
(
|
|
| ||
| 2 |
（2）
|
（其中θ为
| AQ |
| BC |
| BP |
| CQ |
（3）由于B
| P |
| Q |
| P |
| B |
| P |
| B |
| Q |
| C |
| P |
| B |
| C |
| Q |
| P |
| P |
| Q |
| P |
| B |
| P |
| B |
| P |
| C |
| P |
| B |
| C |
| P |
| B |
| C |
| B |
| C |
| B |
| C |
| P |
所以B
| P |
| Q |
| P |
| B |
| P |
| B |
| C |
| P |
| Q |
| P |
| B |
点评：本小题主要考查向量的模、最小值问题中的应用、平面向量数量积的运算等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
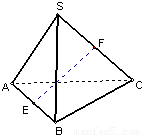
如图，S是边长为a的正三角ABC所在平面外一点，SA=SB=SC=a，E、F是AB和SC的中点，则异面直线SA与EF所成的角为
，延长CB到D，使CB＝BD．
