题目内容
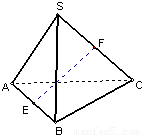
如图，S是边长为a的正三角ABC所在平面外一点，SA=SB=SC=a，E、F是AB和SC的中点，则异面直线SA与EF所成的角为45°
45°
．分析：利用中位线的平行关系将异面直线转化为在同一个平面内的相交直线，然后求夹角．
解答：
解：取AC的中点O，连接EO，FO，取BC的中点P，连接SP，AP，
∵S为正三角形所在平面ABC外一点，且SA=SB=SC=AB=a，
∴SP⊥BC，AP⊥BC，
∴BC⊥平面ASP，
∴BC⊥AS．
∵E、F分别为SC、AB中点，
∴所以OF，OE分别是中位线，所以OE∥SA，OE∥BC，且OE=
SA=
a，OE=
BC=
a，
∴EO⊥FO，且EO=FO，∠FEO是异面直线EF与SA所成角，
∴∠FEO=45°．
故答案为：45°．
解：取AC的中点O，连接EO，FO，取BC的中点P，连接SP，AP，∵S为正三角形所在平面ABC外一点，且SA=SB=SC=AB=a，
∴SP⊥BC，AP⊥BC，
∴BC⊥平面ASP，
∴BC⊥AS．
∵E、F分别为SC、AB中点，
∴所以OF，OE分别是中位线，所以OE∥SA，OE∥BC，且OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EO⊥FO，且EO=FO，∠FEO是异面直线EF与SA所成角，
∴∠FEO=45°．
故答案为：45°．
点评：本题考查异面直线所成的角的求法，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
练习册系列答案
相关题目
如图，正三棱锥S-ABC的侧面是边长为a的正三角形，D是SA的中点，E是BC的中点，求△SDE绕直线SE旋转一周所得到的旋转体的体积．
