题目内容
11.顶点在原点且以双曲线$\frac{x^2}{3}-{y^2}=1$的左准线为准线的抛物线方程是y2=6x.分析 先根据双曲线方程求出其左准线,然后设出抛物线的标准方程进而根据$\frac{p}{2}$=$\frac{3}{2}$可求出P的值,代入得到答案.
解答 解:由双曲线$\frac{x^2}{3}-{y^2}=1$的左准线为x=-$\frac{3}{2}$,
设顶点在原点且以双曲线$\frac{x^2}{3}-{y^2}=1$的左准线为准线的抛物线方程为y2=2px(p>0),
则$\frac{p}{2}$=$\frac{3}{2}$,
所以抛物线方程是y2=6x.
故答案为:y2=6x.
点评 本题主要考查抛物线的标准方程和双曲线的简单性质.考查基础知识的综合运用.

练习册系列答案
相关题目
2.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是( )
| A. | ②、③都不能为系统抽样 | B. | ②、④都不能为分层抽样 | ||
| C. | ①、④都可能为系统抽样 | D. | ①、③都可能为分层抽样 |
6.为了了解市民的环保意识,某校高一(1)班50名学生在6月5日(世界环境日)这一天调查了各自家庭丢弃旧塑料袋的情况,有关数据如下表:
(1)求这50户居民每天丢弃旧塑料袋的平均数;
(2)求这50户居民每天丢弃旧塑料袋的方差.
| 每户丢弃旧塑料袋个数 | 2 | 3 | 4 | 5 |
| 户数 | 10 | 10 | 20 | 10 |
(2)求这50户居民每天丢弃旧塑料袋的方差.
16.已知点O在△ABC内部一点,且满足2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$,则三角形△AOB,△BOC,△AOC的面积之比依次为( )
| A. | 4:2:3 | B. | 2:3:4 | C. | 4:3:2 | D. | 3:4:5 |
20.在△ABC中,角A,B,C的对边分别为a,b,c,设p:“a:b:c=A:B:C”,q:“△ABC是正三角形”,则( )
| A. | p是q的充分不必要条件 | B. | p是q的必要但不充分条件 | ||
| C. | p是q的充要条件 | D. | p是q的既不充分也不必要条件 |
1.如图给定的是纸盒的外表面,下列哪一项能由它折叠而成( )


| A. | 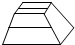 | B. |  | C. |  | D. | 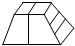 |
 已知向量$\overrightarrow{m}=(3sinx.\frac{\sqrt{3}}{2}cosx),\overrightarrow{n}=(cosx-\frac{\sqrt{3}}{2}sinx,3cosx)$,函数f(x)=$\overrightarrow{m}•\overrightarrow{n}$.
已知向量$\overrightarrow{m}=(3sinx.\frac{\sqrt{3}}{2}cosx),\overrightarrow{n}=(cosx-\frac{\sqrt{3}}{2}sinx,3cosx)$,函数f(x)=$\overrightarrow{m}•\overrightarrow{n}$.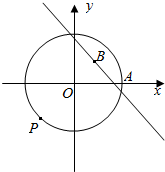 点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.
点A(2,0)是圆x2+y2=4上的定点,点B(1,1)是圆内一点,P为圆上的动点.