题目内容
f(x)=x3-x2-x的单调减区间是
- A.(-∞,-
 )
) - B.(1,+∞)
- C.(-∞,-
 ),(1,+∝)
),(1,+∝) - D.(-
 ,1)
,1)
D
分析:求出导函数;令导函数小于0,求出自变量的范围即为函数的单调递减区间.
解答:f'(x)=3x2-2x-1,
解3x2-2x-1<0得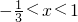 ,
,
所以单调区间是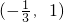
故选D
点评:本题考查函数的单调性与导函数符号的关系:f′(x)>0则f(x)单增;当f′(x)<0则f(x)递减.
分析:求出导函数;令导函数小于0,求出自变量的范围即为函数的单调递减区间.
解答:f'(x)=3x2-2x-1,
解3x2-2x-1<0得
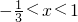 ,
,所以单调区间是
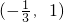
故选D
点评:本题考查函数的单调性与导函数符号的关系:f′(x)>0则f(x)单增;当f′(x)<0则f(x)递减.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目