题目内容
若函数y=f(x)在区间[a,b]上是连续的、单调的函数,且满足f(a)•f(b)<0,则函数y=f(x)在区间[a,b]上有唯一的零点”.对于函数f(x)=-x3+x2+x+m,(1)当m=0时,讨论函数f(x)=-x3+x2+x+m在定义域内的单调性并求出极值;
(2)若函数f(x)=-x3+x2+x+m有三个零点,求实数m的取值范围.
分析:(1)直接求函数f(x)=-x3+x2+x的导函数,判断单调性求函数极值即可;
(2)三次函数有三个零点,也就是函数图象与x轴有三个交点,函数的极小值小于0,极大值大于0,即求函数的极值即可解决.
(2)三次函数有三个零点,也就是函数图象与x轴有三个交点,函数的极小值小于0,极大值大于0,即求函数的极值即可解决.
解答:解:(1)当m=0时,f(x)=-x3+x2+x.
∴f′(x)=-3x2+2x+1=-3(x+
)(x-1).
列表如下:
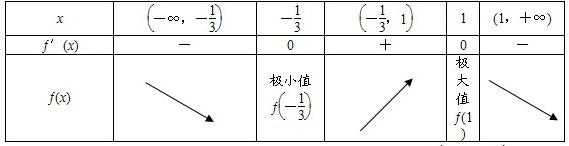
由表可知:函数f(x)=-x3+x2+x在区间[-
,1]上单调递增,在(-∞,-
)和(1,+∞)上单调递减.
∴f(x)的极小值为f(-
)=-
,
极大值为?(1)=1.
(2)由(1)知,当x=-
时,
f(x)取得极小值f(-
)=
+
-
+m=m-
,
当x=1时,f(x)取得极大值
f(1)=-1+1+1+m=m+1,
当
,即-1<m<
时,
f(-1)=1+1-1+m=m+1>0,
f(-
)=m-
<0,
f(1)=m+1>0,f(2)=m-2<0,
∴f(x)=-x3+x2+m在[-1,-
]上有唯一零点.
在(-
,1]上有唯一零点,在(1,2]上有唯一零点.又f(x)=-x3+x2+x+m在(-∞,-1]上单调递减,
在[2,+∞]上单调递减,∴在(-∞,-1]上恒有?f(x)≥f(-1)>0,在[2,+∞)上恒有f(x)≤f(2)<0.
∴f(x)=-x3+x2+x+m-在(-∞,-1]和[2,+∞)上无零点.∴-1<m<
时,函数f(x)=-x3+x2+x+m在有三个零点,
∴所求实数m的取值范围是(-1,
).
∴f′(x)=-3x2+2x+1=-3(x+
| 1 |
| 3 |
列表如下:

由表可知:函数f(x)=-x3+x2+x在区间[-
| 1 |
| 3 |
| 1 |
| 3 |
∴f(x)的极小值为f(-
| 1 |
| 3 |
| 5 |
| 27 |
极大值为?(1)=1.
(2)由(1)知,当x=-
| 1 |
| 3 |
f(x)取得极小值f(-
| 1 |
| 3 |
| 1 |
| 27 |
| 1 |
| 9 |
| 1 |
| 3 |
| 5 |
| 27 |
当x=1时,f(x)取得极大值
f(1)=-1+1+1+m=m+1,
当
|
| 5 |
| 27 |
f(-1)=1+1-1+m=m+1>0,
f(-
| 1 |
| 3 |
| 5 |
| 27 |
f(1)=m+1>0,f(2)=m-2<0,
∴f(x)=-x3+x2+m在[-1,-
| 1 |
| 3 |
在(-
| 1 |
| 3 |
在[2,+∞]上单调递减,∴在(-∞,-1]上恒有?f(x)≥f(-1)>0,在[2,+∞)上恒有f(x)≤f(2)<0.
∴f(x)=-x3+x2+x+m-在(-∞,-1]和[2,+∞)上无零点.∴-1<m<
| 5 |
| 27 |
∴所求实数m的取值范围是(-1,
| 5 |
| 27 |
点评:本题考查函数的导数研究函数的单调性,函数零点的概念,以及函数的导数求函数的极值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目