题目内容
如图，已知点A（0，2）和抛物线y2=x+4上两点B、C，使得AB⊥BC，求点C的纵坐标的取值范围．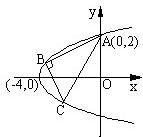
设B（y12-4，y1）、C（y2-4，y），显然y12-4≠0，故kAB=
=
由于AB⊥BC，∴kBC=-（y1+2），从而
消去x，注意到y≠y1，得（2+y1）（y+y1）+1=0?y12+（2+y）y1+（2y+1）=0，∵
由△≥0，解得y≤0或y≥4，
当y=0时，点B的坐标为（-3，-1），当y=4时，点B的坐标为（5，-3），均满足题意，
故点C的纵坐标的取值范围是y≤0或y≥4．
| y1-2 |
| y12-4 |
| 1 |
| y1+2 |
由于AB⊥BC，∴kBC=-（y1+2），从而
|
消去x，注意到y≠y1，得（2+y1）（y+y1）+1=0?y12+（2+y）y1+（2y+1）=0，∵
由△≥0，解得y≤0或y≥4，
当y=0时，点B的坐标为（-3，-1），当y=4时，点B的坐标为（5，-3），均满足题意，
故点C的纵坐标的取值范围是y≤0或y≥4．
练习册系列答案
相关题目
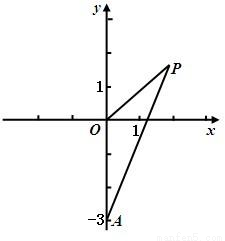
如图，已知点A（0，-3），动点P满足|PA|=2|PO|，其中O为坐标原点．
如图，已知点A（0，2）和抛物线y2=x+4上两点B、C，使得AB⊥BC，求点C的纵坐标的取值范围．
；
；
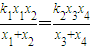