题目内容
已知F1、F2分别是椭圆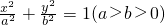 的左、右焦点,P是此椭圆上的一动点,并且
的左、右焦点,P是此椭圆上的一动点,并且 的取值范围是
的取值范围是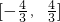 .
.
(Ⅰ)求此椭圆的方程;
(Ⅱ)点A是椭圆的右顶点,直线y=x与椭圆交于B、C两点(C在第一象限内),又P、Q是椭圆上两点,并且满足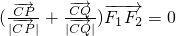 ,求证:向量
,求证:向量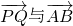 共线.
共线.
解:(Ⅰ)设P(x0,y0),F1(-c,0),F2(c,0),
其中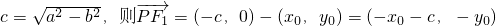 ,
,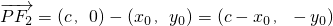 .
.
从而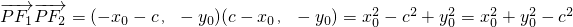 .
.
由于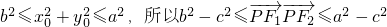 ,
,
即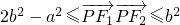 .
.
又已知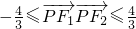 ,
,
所以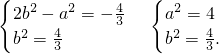
从而椭圆的方程是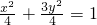 .
.
(Ⅱ)因为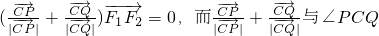 的平分线平行,
的平分线平行,
所以∠PCQ的平分线垂直于x轴.
由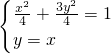
解得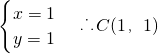 .
.
不妨设PC的斜率为k,则QC的斜率为-k,
因此PC和QC的方程分别为y=k(x-1)+1,y=-k(x-1),
其中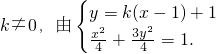
消去y并整理得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*).
∵C(1,1)在椭圆上,
∴x=1是方程(*)的一个根.
从而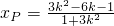 ,同理
,同理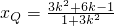 ,
,
从而直线PQ的斜率为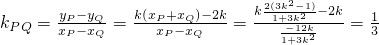 .
.
又知A(2,0),B(-1,-1),
所以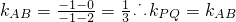 ,
,
∴向量 与
与 共线.
共线.
分析:(I)由题意设P(x0,y0),F1(-c,0),F2(c,0)利用 的取值范围所以∠PCQ的平分线垂直于x轴.是
的取值范围所以∠PCQ的平分线垂直于x轴.是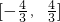 ,得到a,b的方程,求解即可;
,得到a,b的方程,求解即可;
(II)有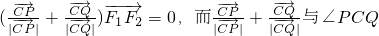 的平分线平行,所以∠PCQ的平分线垂直于x轴,进而建立方程,解出C点,再设出PC方程进而得到QC的方程,把它与椭圆方程联立得到直线PQ的斜率,与直线AB比较即可求证.
的平分线平行,所以∠PCQ的平分线垂直于x轴,进而建立方程,解出C点,再设出PC方程进而得到QC的方程,把它与椭圆方程联立得到直线PQ的斜率,与直线AB比较即可求证.
点评:(I)此问考查了设处点的坐标,把已知的向量关系的等式建立成坐标之间的关系式,还考查了椭圆的基本性质及求解时运用的方程的思想;
(II)此问考查了设出直线把椭圆方程与直线方程进行联立,利用根与系数的关系求出P与Q的坐标,还考查了直线的斜率公式.
其中
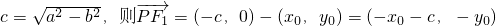 ,
,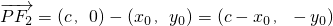 .
.从而
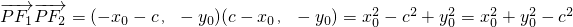 .
.由于
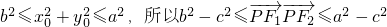 ,
,即
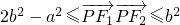 .
.又已知
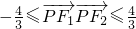 ,
,所以
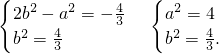
从而椭圆的方程是
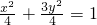 .
.(Ⅱ)因为
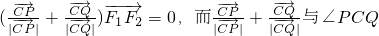 的平分线平行,
的平分线平行,所以∠PCQ的平分线垂直于x轴.
由
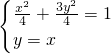
解得
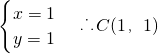 .
.不妨设PC的斜率为k,则QC的斜率为-k,
因此PC和QC的方程分别为y=k(x-1)+1,y=-k(x-1),
其中
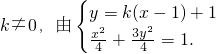
消去y并整理得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*).
∵C(1,1)在椭圆上,
∴x=1是方程(*)的一个根.
从而
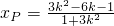 ,同理
,同理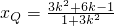 ,
,从而直线PQ的斜率为
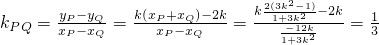 .
.又知A(2,0),B(-1,-1),
所以
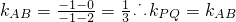 ,
,∴向量
 与
与 共线.
共线.分析:(I)由题意设P(x0,y0),F1(-c,0),F2(c,0)利用
 的取值范围所以∠PCQ的平分线垂直于x轴.是
的取值范围所以∠PCQ的平分线垂直于x轴.是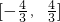 ,得到a,b的方程,求解即可;
,得到a,b的方程,求解即可;(II)有
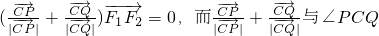 的平分线平行,所以∠PCQ的平分线垂直于x轴,进而建立方程,解出C点,再设出PC方程进而得到QC的方程,把它与椭圆方程联立得到直线PQ的斜率,与直线AB比较即可求证.
的平分线平行,所以∠PCQ的平分线垂直于x轴,进而建立方程,解出C点,再设出PC方程进而得到QC的方程,把它与椭圆方程联立得到直线PQ的斜率,与直线AB比较即可求证.点评:(I)此问考查了设处点的坐标,把已知的向量关系的等式建立成坐标之间的关系式,还考查了椭圆的基本性质及求解时运用的方程的思想;
(II)此问考查了设出直线把椭圆方程与直线方程进行联立,利用根与系数的关系求出P与Q的坐标,还考查了直线的斜率公式.

练习册系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: