题目内容
山姆的意大利馅饼屋中设有一个投镖靶该靶为正方形板.边长为18厘米,挂于前门附近的墙上,顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利馅饼中的一个,投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆域时.可得到一个大馅饼;当击中半径为1厘米到2厘米之间的环域时,可得到一个中馅饼;如果击中半径为2厘米到3厘米之间的环域时,可得到一个小馅饼,如果击中靶上的其他部分,则得不到谄饼,我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖不会击中线上,试求一顾客将嬴得:
(1)一张大馅饼的概率;
(2)一张中馅饼的概率;
(3)一张小馅饼的概率;
(4)没得到馅饼的概率.
(1)一张大馅饼的概率;
(2)一张中馅饼的概率;
(3)一张小馅饼的概率;
(4)没得到馅饼的概率.

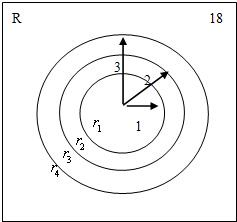
我们实验的样本空间可由一个边长为18的正方形表示.
如图表明R和子区域r1、r2、r3和r,它们分别表示得大馅饼、中馅饼、小馅饼或没得到馅饼的事件.
(1)P(r1)=
=
=
≈0.01;
(2)P(r2)=
=
=
≈0.03;
(3)P(r3)=
=
=
≈0.05;
(4)P(r)=
=
≈0.91

如图表明R和子区域r1、r2、r3和r,它们分别表示得大馅饼、中馅饼、小馅饼或没得到馅饼的事件.
(1)P(r1)=
| r1的面积 |
| R的面积 |
| π(1)2 |
| 182 |
| π |
| 324 |
(2)P(r2)=
| r2的面积 |
| R的面积 |
| π(2)2-π(1)2 |
| 324 |
| 3π |
| 324 |
(3)P(r3)=
| r3的面积 |
| R的面积 |
| π(3)2-π(2)2 |
| 324 |
| 5π |
| 324 |
(4)P(r)=
| r的面积 |
| R的面积 |
| 324-π(3)2 |
| 324 |


练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目