题目内容
(本题满分14分)本题共有2个小题,第(1)小题满分5分,第(2)小题满分9分.
设双曲线 ,
, 是它实轴的两个端点,
是它实轴的两个端点, 是其虚轴的一个端点.已知其一条渐近线的一个方向向量是
是其虚轴的一个端点.已知其一条渐近线的一个方向向量是 ,
, 的面积是
的面积是 ,
, 为坐标原点,直线
为坐标原点,直线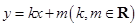 与双曲线C相交于
与双曲线C相交于 、
、 两点,且
两点,且 .
.
(1)求双曲线 的方程;
的方程;
(2)求点 的轨迹方程,并指明是何种曲线.
的轨迹方程,并指明是何种曲线.
【答案】
解:(1) (理)由题意,双曲线的渐近线方程为 ,则有
,则有
又 的面积是
的面积是 ,故
,故 ,得
,得 (3分)
(3分)
所以双曲线 的方程为
的方程为 .
(6分)
.
(6分)
(2)设 ,直线
,直线 :
: 与双曲线
与双曲线 联立消去
联立消去 ,
,
得 由题意
由题意 , (2分)
, (2分)
且 (4分)
(4分)
又由 知
知
而
所以
化简得 ①
①
由 可得
可得 ②
②
由①②可得 (6分)
(6分)
故点P的轨迹方程是 (8分)
(8分)
【解析】略

练习册系列答案
相关题目
 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本) 年销售量.
年销售量. 与投入成本增加的比例
与投入成本增加的比例 的关系式;
的关系式;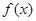 =
=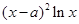 ,
,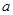 ∈R
∈R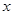 =
=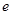 为
为 的极值点,求实数
的极值点,求实数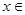 (0,3
(0,3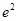 成立.
成立.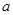 元,每期利率为
元,每期利率为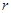 ,设存期为
,设存期为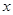 ,本利和(本金加上利息)为
,本利和(本金加上利息)为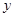 元。
元。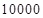 元,每期利率为
元,每期利率为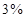 ,试计算
,试计算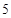 期后的本利和。
期后的本利和。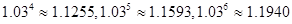 )
) 中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
,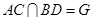 .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: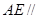 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.