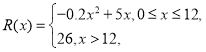题目内容
【题目】已知函数![]() ,且
,且![]() .
.
(Ⅰ)若![]() 是关于
是关于![]() 的方程
的方程![]() 的一个解,求
的一个解,求![]() 的值;
的值;
(Ⅱ)当![]() 且
且![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅲ)若函数![]() 在区间
在区间![]() 上有零点,求
上有零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 取值范围为:
取值范围为:![]() 或
或![]() .
.
【解析】
试题分析:(Ⅰ)由题意得![]() ,从而解得;(Ⅱ)由题意得
,从而解得;(Ⅱ)由题意得![]() ,由对数函数的单调性可得
,由对数函数的单调性可得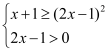 ,从而解得;(Ⅲ)化简
,从而解得;(Ⅲ)化简![]() ,从而令
,从而令![]() ,讨论可得
,讨论可得![]() ,从而解得.
,从而解得.
试题解析:(Ⅰ)![]() 是方程式
是方程式![]() 的解
的解
![]()
![]()
又![]()
![]()
![]()
(Ⅱ)![]() 时,
时,![]() 又
又![]()
![]()
![]()
![]()
![]() 解集为:
解集为:![]()
(Ⅲ)解法一:![]()
由![]() 得:
得:![]()
![]()
设![]() ,则
,则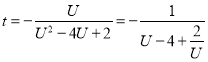
令![]()
![]() 当
当![]() 时,
时,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() 是增函数,且
是增函数,且![]() .
.
![]() 且
且![]() .
.
![]() 或
或![]() ,
,
![]() 取值范围为:
取值范围为:![]() 或
或![]() .
.
解法二:若![]() ,则
,则![]() 在
在![]() 上没有零点.下面就
上没有零点.下面就![]() 时分三种情况讨论:
时分三种情况讨论:
①方程![]() 在
在![]() 上有重根
上有重根![]() ,则
,则![]() ,解得:
,解得:![]()
又![]() .
.
②![]() 在
在![]() 上只有一个零点,且不是方程的重根,则有
上只有一个零点,且不是方程的重根,则有![]()
解得:![]() 或
或 ![]() 又经检验:
又经检验:![]() 或
或![]() 时,
时,![]() 在
在![]() 上都有零点;
上都有零点;
![]() 或
或![]()
③方程![]() 在
在![]() 上有两个相异实根,则有:
上有两个相异实根,则有:
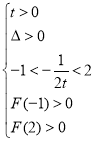 或
或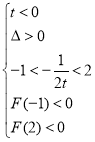 解得:
解得:![]()
综合①②③可知:![]() 取值范围为
取值范围为![]() 或
或![]() .
.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
【题目】某产品按行业生产标准分成![]() 个等级,等级系数
个等级,等级系数![]() 依次
依次![]() ,其中
,其中![]() 为标准
为标准![]() ,
,![]() 为标准
为标准![]() .已知甲厂执行标准
.已知甲厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件;乙厂执行标准
元/件;乙厂执行标准![]() 生产该产品,产品的零售价为
生产该产品,产品的零售价为![]() 元/件,假定甲、乙两厂的产品都符合相应的执行标准.
元/件,假定甲、乙两厂的产品都符合相应的执行标准.
(1)已知甲厂产品的等级系数![]() 的概率分布如下所示:
的概率分布如下所示:
|
|
|
|
|
|
|
|
|
|
且![]() 的数学期望
的数学期望![]() ,求
,求![]() 的值;
的值;
(2)为分析乙厂产品的等级系数![]() ,从该厂生产的产品中随机抽取
,从该厂生产的产品中随机抽取![]() 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:

用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数![]() 的数学期望;
的数学期望;
(3)在(1)、(2)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.注:①产品的“性价比”![]() ;
;
②“性价比”大的产品更具可购买性.