题目内容
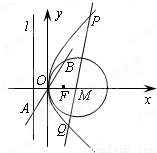
 (文)已知抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为
(文)已知抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为| π |
| 3 |
(Ⅰ)求⊙M和抛物线C的标准方程;
(Ⅱ)过圆心M的直线交抛物线C于P、Q两点,问
| OP |
| OQ |
分析:(Ⅰ)根据
=OA•cos60°,可求出p的值,从而求出抛物线方程,求出圆心和半径可求出⊙M的方程;
(Ⅱ)分类讨论,设出直线方程代入抛物线方程,利用韦达定理及向量的数量积公式,即可求得结论.
| p |
| 2 |
(Ⅱ)分类讨论,设出直线方程代入抛物线方程,利用韦达定理及向量的数量积公式,即可求得结论.
解答:解:(Ⅰ)因为
=OA•cos60°=2×
=1,即p=2,所以抛物线C的方程为y2=4x
设⊙M的半径为r,则r=
×
=2,所以⊙M的方程为(x-2)2+y2=4
(Ⅱ)M(2,0),设P(x1,y1),Q(x2,y2),
(1)当PQ斜率不存在时,P(2,2
),Q(2,-2
),则
•
=x1x2+y1y2=-4
(2)当PQ斜率存在时,设PQ的方程为y=k(x-2)(k≠0),消y得k2x2-(4k2+4)x+4k2=0
所以x1+x2=
,x1x2=4,
因为y12=4x1,y22=4x2,所以y12y22=16x1x2=64,故y1y2=-8
所以
•
=x1x2+y1y2=-4
所以
•
为定值,该值为-4.
| p |
| 2 |
| 1 |
| 2 |
设⊙M的半径为r,则r=
| OB |
| 2 |
| 1 |
| cos60° |
(Ⅱ)M(2,0),设P(x1,y1),Q(x2,y2),
(1)当PQ斜率不存在时,P(2,2
| 2 |
| 2 |
| OP |
| OQ |
(2)当PQ斜率存在时,设PQ的方程为y=k(x-2)(k≠0),消y得k2x2-(4k2+4)x+4k2=0
所以x1+x2=
| 4k2+4 |
| k2 |
因为y12=4x1,y22=4x2,所以y12y22=16x1x2=64,故y1y2=-8
所以
| OP |
| OQ |
所以
| OP |
| OQ |
点评:本题考查抛物线与圆的方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
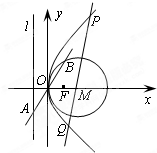 (文)已知抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为
(文)已知抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为 的直线,交l于点A,交⊙M于另一点B,且AO=OB=2.
的直线,交l于点A,交⊙M于另一点B,且AO=OB=2. 是否为定值,若是定值,求出该定值.
是否为定值,若是定值,求出该定值.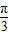 的直线,交l于点A,交⊙M于另一点B,且AO=OB=2.
的直线,交l于点A,交⊙M于另一点B,且AO=OB=2.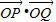 是否为定值,若是定值,求出该定值.
是否为定值,若是定值,求出该定值.