题目内容
【题目】设集合![]() .若
.若![]() 的非空子集
的非空子集![]() 中奇数的个数大于偶数的个数,则称
中奇数的个数大于偶数的个数,则称![]() 是“好的”.试求
是“好的”.试求![]() 的所有“好的”子集的个数(答案写成最简结果).
的所有“好的”子集的个数(答案写成最简结果).
【答案】见解析
【解析】
对![]() 分奇、偶两种情况讨论.
分奇、偶两种情况讨论.
(1)当![]() (
(![]() 为非负整数),这时
为非负整数),这时![]() 中奇元素恰比偶元素多一个.设
中奇元素恰比偶元素多一个.设![]() 是
是![]() 的任何一个子集,则
的任何一个子集,则![]() 和
和![]() 中有且只有一个子集是“好的”,从而
中有且只有一个子集是“好的”,从而![]() 的“好子集”的个数为
的“好子集”的个数为![]() .
.
(2)当![]() (
(![]() 为正整数),
为正整数),![]() 中奇元素个数与偶元素个数相等.定义
中奇元素个数与偶元素个数相等.定义![]() 为“坏子集”为当且仅当
为“坏子集”为当且仅当![]() 中奇元素个数小于偶元素的个数,而定义
中奇元素个数小于偶元素的个数,而定义![]() 为“中性子集”(包括空集)为当且仅当
为“中性子集”(包括空集)为当且仅当![]() 中奇元素个数与偶元素个数相等.
中奇元素个数与偶元素个数相等.
由对称性知,![]() 的“好子集”个数与“坏子集”的个数必定相等,所以有
的“好子集”个数与“坏子集”的个数必定相等,所以有
“好子集”个数
![]()
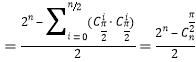 .
.
其中公式![]() 可证明如下:考虑恒等式
可证明如下:考虑恒等式![]() 两边中
两边中![]() 项的系数,由二项式定理知,左边式中
项的系数,由二项式定理知,左边式中![]() 项的系数是
项的系数是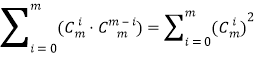 ,而右边式中
,而右边式中![]() 的系数是
的系数是![]() ,故得恒等式
,故得恒等式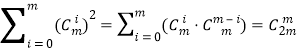 .
.
本题答案可统一地写为![]()
其中![]() 是不大于
是不大于![]() 的最大整数).
的最大整数).
注:由恒等式![]() 可得组合恒等式:
可得组合恒等式:
![]()
![]()
(注意当![]() 时,
时,![]() ).这种利用模型来建立和证明组合恒等式的方法(叫做“模型法”)在组合数学中是很常用的,也很重要,应该熟悉进而掌握它.如果
).这种利用模型来建立和证明组合恒等式的方法(叫做“模型法”)在组合数学中是很常用的,也很重要,应该熟悉进而掌握它.如果![]() 是
是![]() 个奇数和
个奇数和![]() 个偶数组成,那么
个偶数组成,那么![]() 的“好子集”个数又为多少呢?请读者自己考虑之.
的“好子集”个数又为多少呢?请读者自己考虑之.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目