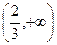题目内容
(本题满分12分)已知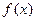 是定义在
是定义在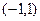 上的奇函数,且当
上的奇函数,且当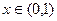 时,
时,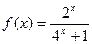 .
.
(1)求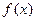 在
在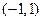 上的解析式;
上的解析式;
(2) 证明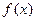 在
在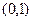 上是减函数;
上是减函数;
(3)当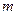 取何值时,
取何值时,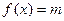 在
在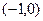 上有解.
上有解.
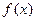 是定义在
是定义在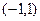 上的奇函数,且当
上的奇函数,且当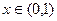 时,
时,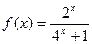 .
.(1)求
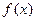 在
在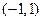 上的解析式;
上的解析式; (2) 证明
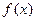 在
在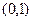 上是减函数;
上是减函数;(3)当
 取何值时,
取何值时,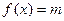 在
在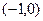 上有解.
上有解.解:设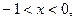 则
则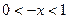 …… 1 分
…… 1 分
∴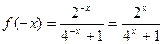 …… 2 分
…… 2 分
∵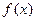 为奇函数 ∴
为奇函数 ∴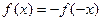
∴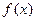
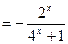 …… 3 分
…… 3 分
又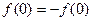 ∴
∴ 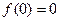 …… 4 分
…… 4 分
综上: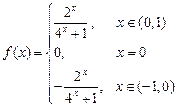 …… 5 分
…… 5 分
(2)(解法一)证明:设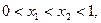
则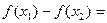
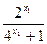 -
-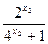 =
=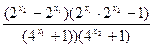 …… 7 分
…… 7 分
∵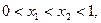 ∴
∴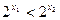 ,
,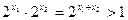 ∴
∴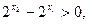
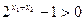 又
又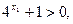
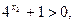
∴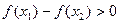 ,
,
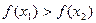
∴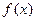 在
在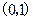 上是减函数. ……
上是减函数. …… 9 分
9 分
(解法二)证明:∵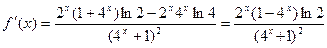 ……7 分
……7 分
∵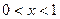 ∴
∴ 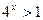 即
即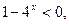 又
又 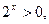
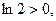
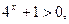
∴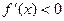 ∴
∴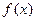 在
在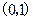 上是减函数. …… 9 分
上是减函数. …… 9 分
(3)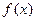 是定义在
是定义在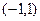 上的奇函数,且由(2)知,
上的奇函数,且由(2)知,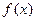 在
在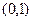 上单调递减
上单调递减
∴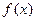 在
在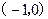 上单调递减,
上单调递减,
∴当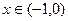 时,有
时,有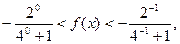 即
即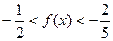 …… 11 分
…… 11 分
∴要使方程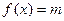 在
在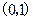 上有解,只需
上有解,只需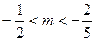 . 故
. 故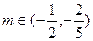 .… 12 分
.… 12 分
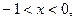 则
则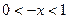 …… 1 分
…… 1 分∴
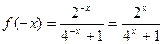 …… 2 分
…… 2 分∵
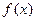 为奇函数 ∴
为奇函数 ∴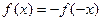
∴
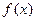
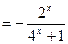 …… 3 分
…… 3 分又
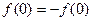 ∴
∴ 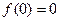 …… 4 分
…… 4 分综上:
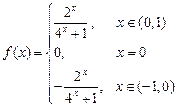 …… 5 分
…… 5 分(2)(解法一)证明:设
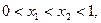
则
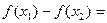
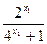 -
-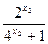 =
=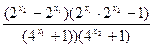 …… 7 分
…… 7 分∵
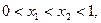 ∴
∴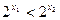 ,
,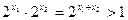 ∴
∴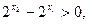
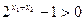 又
又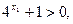
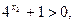
∴
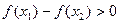 ,
,
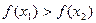
∴
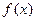 在
在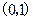 上是减函数. ……
上是减函数. …… 9 分
9 分(解法二)证明:∵
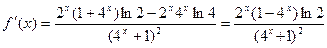 ……7 分
……7 分∵
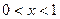 ∴
∴ 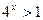 即
即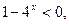 又
又 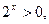
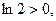
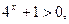
∴
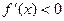 ∴
∴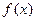 在
在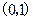 上是减函数. …… 9 分
上是减函数. …… 9 分(3)
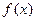 是定义在
是定义在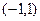 上的奇函数,且由(2)知,
上的奇函数,且由(2)知,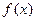 在
在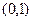 上单调递减
上单调递减∴
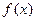 在
在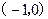 上单调递减,
上单调递减,∴当
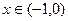 时,有
时,有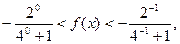 即
即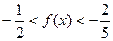 …… 11 分
…… 11 分∴要使方程
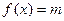 在
在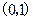 上有解,只需
上有解,只需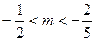 . 故
. 故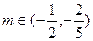 .… 12 分
.… 12 分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
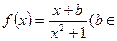 R) 是奇函数,
R) 是奇函数, 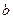 的值;
的值;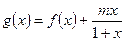 在区间
在区间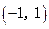 上有且仅有两个不同的零点,求实数
上有且仅有两个不同的零点,求实数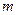 的取值范围.
的取值范围. 知
知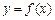 是偶函数,当
是偶函数,当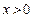 时,
时,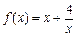 ,且当
,且当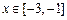 时,
时,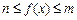 恒成立,则
恒成立,则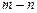 的最小值是( )
的最小值是( )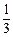
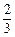
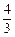
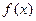 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当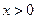 时,
时,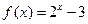 ,则
,则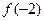 的值等于
的值等于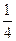
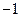
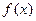 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当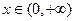 时,
时,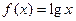 ,则满足
,则满足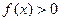 的
的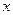 的取值范围是 ( )
的取值范围是 ( )
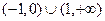
 -1,+∞)
-1,+∞)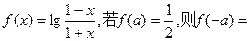 ( )
( )
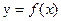 与
与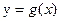 有相同的定义域,且都不是常数函数,对定义域中任意x,有
有相同的定义域,且都不是常数函数,对定义域中任意x,有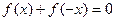 ,
,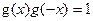 ,且x≠0,
,且x≠0,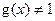 ,则
,则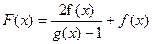 ………………()
………………()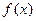 在区间
在区间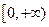 单调递增,则满足
单调递增,则满足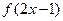 <
<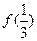 的x 取值范围是
的x 取值范围是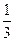 ,
,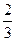 )
)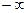 ,
,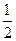 ,
,