题目内容
已知a,b是实数,函数f(x)=x3+ax,g(x)=x2+bx,f′(x)和g′(x)是f(x),g(x)的导函数,若f′(x)g′(x)≥0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性一致,
(1)设a>0,若函数f(x)和g(x)在区间[-1,+∞)上单调性一致,求实数b的取值范围;
(2)设a<0且a≠b,若函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
(1)设a>0,若函数f(x)和g(x)在区间[-1,+∞)上单调性一致,求实数b的取值范围;
(2)设a<0且a≠b,若函数f(x)和g(x)在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
解:(1)因为函数f(x)和g(x)在区间[-1,+∞)上单调性一致,
所以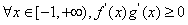 ,
,
即 ,
,
∵a>0,
∴ ,
,
即∵a>0,
∴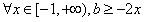 ,
,
∴b≥2;
(2)当b<a时,因为函数f(x)和g(x)在区间(b,a)上单调性一致,
所以, ,
,
即 ,
,
 ,
,
∴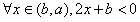 ,
,
∴ ,
,
∴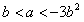 ,
,
设z=a-b,考虑点(b,a)的可行域,函数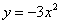 的斜率为1的切线的切点设为
的斜率为1的切线的切点设为 ,
,
则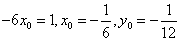 ,
,
∴ ;
;
当a<b<0时,因为函数f(x)和g(x)在区间(a,b)上单调性一致,
所以 ,
,
即 ,
,
∵b<0,∴ ,
,
∴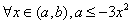 ,∴
,∴ ,
,
∴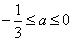 ,∴
,∴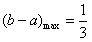 ;
;
当a<0<b时,因为函数f(x)和g(x)在区间(a,b)上单调性一致,
所以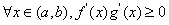 ,
,
即 ,
,
∵b>0,而x=0时, 不符合题意;
不符合题意;
当a<0=b时,由题意: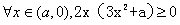 ,
,
∴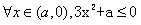 ,∴
,∴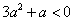 ,
,
∴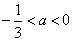 ,∴
,∴ ;
;
综上可知,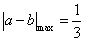 。
。
所以
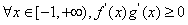 ,
,即
 ,
,∵a>0,
∴
 ,
,即∵a>0,
∴
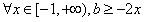 ,
,∴b≥2;
(2)当b<a时,因为函数f(x)和g(x)在区间(b,a)上单调性一致,
所以,
 ,
,即
 ,
, ,
,∴
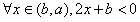 ,
,∴
 ,
,∴
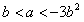 ,
,设z=a-b,考虑点(b,a)的可行域,函数
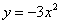 的斜率为1的切线的切点设为
的斜率为1的切线的切点设为 ,
,则
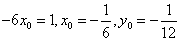 ,
,∴
 ;
;当a<b<0时,因为函数f(x)和g(x)在区间(a,b)上单调性一致,
所以
 ,
,即
 ,
,∵b<0,∴
 ,
,∴
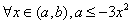 ,∴
,∴ ,
,∴
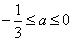 ,∴
,∴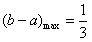 ;
;当a<0<b时,因为函数f(x)和g(x)在区间(a,b)上单调性一致,
所以
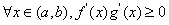 ,
,即
 ,
,∵b>0,而x=0时,
 不符合题意;
不符合题意;当a<0=b时,由题意:
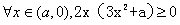 ,
,∴
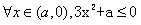 ,∴
,∴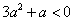 ,
,∴
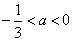 ,∴
,∴ ;
;综上可知,
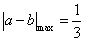 。
。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a-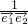 是偶函数.
是偶函数. =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a- 是偶函数.
是偶函数.