题目内容

【题目】已知函数f（x）= ，若方程f（x）=a有四个不同的解x1 ， x2 ， x3 ， x4 ， 且x1＜x2＜x3＜x4 ， 则x3（x1+x2）+ 的取值范围是（ ）
A.（﹣1，+∞）
B.（﹣1，1]
C.（﹣∞，1）
D.[﹣1，1）

【答案】B
【解析】解：作函数f（x）= ，的图象如下，

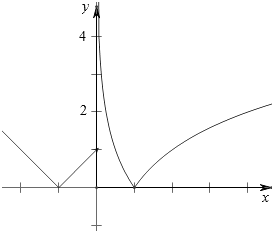
由图可知，x1+x2=﹣2，x3x4=1；1＜x4≤2；

故x3（x1+x2）+ =﹣ +x4，

其在1＜x4≤2上是增函数，

故﹣2+1＜﹣ +x4≤﹣1+2；

即﹣1＜﹣ +x4≤1；

故选B．

作函数f（x）= 的图象如下，由图象可得x1+x2=﹣2，x3x4=1；1＜x4≤2；从而化简x3（x1+x2）+ ，利用函数的单调性求取值范围．

练习册系列答案
相关题目

【题目】已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0， ）的部分图象如图所示
（Ⅰ）求A，ω，φ的值；
（Ⅱ）求f（x）的单调增区间．

【题目】椭圆H： +y2=1（a＞1），原点O到直线MN的距离为 ，其中点M（0，﹣1），点N（a，0）．
（1）求该椭圆H的离心率e；
（2）经过椭圆右焦点F2的直线l和该椭圆交于A，B两点，点C在椭圆上，O为原点， 若 = + ，求直线l的方程．

【题目】已知函数 f（x）=ex（ex﹣a）﹣a2x．
（1）讨论 f（x）的单调性；
（2）若f（x）≥0，求a的取值范围．

【题目】对于区间，若函数同时满足：①在上是单调函数；②函数， 的值域是，则称区间为函数的“保值”区间．

（）求函数的所有“保值”区间．

（）函数是否存在“保值”区间？若存在，求出的取值范围；若不存在，说明理由．

【题目】若函数f（x）=lnx﹣x﹣mx在区间[1，e2]内有唯一的零点，则实数m的取值范围是 ．

【题目】已知U={y|y=log2x，x＞1}，P={y|y= ，x＞2}，则UP=（ ）
A.[ ，+∞）
B.（0， ）
C.（0，+∞）
D.（﹣∞，0）∪（ ，+∞）

【题目】已知函数， .

（1）当时，求函数的值域；

（2）如果对任意的，不等式恒成立，求实数的取值范围；

（3）是否存在实数，使得函数的最大值为0，若存在，求出的值，若不存在，说明理由.

【题目】已知数列{an}中，a1=1，an+1= （n∈N*）．
（1）求证：{ + }是等比数列，并求{an}的通项公式an；
（2）数列{bn}满足bn=（3n﹣1） an ， 数列{bn}的前n项和为Tn ， 若不等式（﹣1）nλ＜Tn+ 对一切n∈N*恒成立，求λ的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网