题目内容
某市2009年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长5%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.以2009年为第一年,那么,到哪一年底,
(Ⅰ)该市历年所建中低价房的累计面积将首次不少于4750万平方米?
(Ⅱ)所有建造的中低价房的面积占建造总住房面积的比例首次大于75%?
(附:可参考数据:1.052=1.103,1.053=1.158,1.054=1.216,1.055=1.276;1.056=1.340)
解:(Ⅰ)设中低价房面积形成数列an,由题意可知an是等差数列,
其中a1=250,d=50,则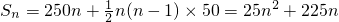 ,(2分)
,(2分)
令25n2+225n≥4750,即n2+9n-190≥0,而n是正整数,∴n≥10.(4分)
到2018年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.(5分)
(Ⅱ)第n年所建造的中低价房面积为an,新建住房面积为bn,n内新建住房总面积为Sn,
中低价住房总面积为Tn,则an=50n+200,bn=400×1.5n-1,(6分)
所以Sn=400+400×1.05+400×1.052++400×1.05n-1=8000(1.05n-1)(7分)
Tn=250+300+350++50n+200=25n2+225n,(9分)
依题意:Tn>0.75Sn,∴8000(1.05n-1)×0.75<25n2+225n(10分)n
=1,2,3时,Tn<0.75Sn,n=4时,Tn>0.75Sn(12分)
到2012年底所有建造的中低价房的面积占建造总住房面积的比例首次大于75%(13分)
分析:(Ⅰ)设中低价房面积形成数列{an},由题意可知{an}是等差数列,求得首项和公差,利用等差数列的求和公式求得Sn,进而根据Sn≥4750,求得n的最小值.
(Ⅱ)设新建住房面积形成数列{bn},由题意可知{bn}是等比数列,根据题意可求得数列的首项和公比,则数列的通项公式可得,求出其前n项和Tn进而Tn>0.75Sn,求得n的最小正整数.
点评:本题主要考查了数列的应用.解题的关键是利用题设条件判断出数列的类型,根据等差或等比数列的性质来解决.
其中a1=250,d=50,则
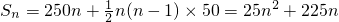 ,(2分)
,(2分)令25n2+225n≥4750,即n2+9n-190≥0,而n是正整数,∴n≥10.(4分)
到2018年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.(5分)
(Ⅱ)第n年所建造的中低价房面积为an,新建住房面积为bn,n内新建住房总面积为Sn,
中低价住房总面积为Tn,则an=50n+200,bn=400×1.5n-1,(6分)
所以Sn=400+400×1.05+400×1.052++400×1.05n-1=8000(1.05n-1)(7分)
Tn=250+300+350++50n+200=25n2+225n,(9分)
依题意:Tn>0.75Sn,∴8000(1.05n-1)×0.75<25n2+225n(10分)n
=1,2,3时,Tn<0.75Sn,n=4时,Tn>0.75Sn(12分)
到2012年底所有建造的中低价房的面积占建造总住房面积的比例首次大于75%(13分)
分析:(Ⅰ)设中低价房面积形成数列{an},由题意可知{an}是等差数列,求得首项和公差,利用等差数列的求和公式求得Sn,进而根据Sn≥4750,求得n的最小值.
(Ⅱ)设新建住房面积形成数列{bn},由题意可知{bn}是等比数列,根据题意可求得数列的首项和公比,则数列的通项公式可得,求出其前n项和Tn进而Tn>0.75Sn,求得n的最小正整数.
点评:本题主要考查了数列的应用.解题的关键是利用题设条件判断出数列的类型,根据等差或等比数列的性质来解决.

练习册系列答案
相关题目
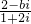 (b∈R)的实部与虚部互为相反数,则b=
(b∈R)的实部与虚部互为相反数,则b=


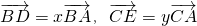 ,x>0,y>0,且x+y=1,则
,x>0,y>0,且x+y=1,则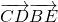 的最大值为
的最大值为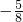




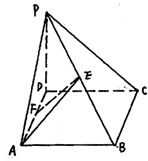 如图,在四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,E、F分别是PB、AD的中点,PD=2.
如图,在四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,E、F分别是PB、AD的中点,PD=2.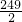
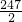
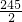
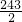
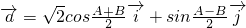 ,其中
,其中 、
、 为互相垂直的单位向量,若
为互相垂直的单位向量,若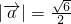 .求tanA•tanB的值.
.求tanA•tanB的值.

