题目内容
【题目】已知数列{an}，{bn}满足2Sn=（an+2）bn ， 其中Sn是数列{an}的前n项和．
（1）若数列{an}是首项为 
，公比为﹣ 
的等比数列，求数列{bn}的通项公式；
（2）若bn=n，a2=3，求证：数列{an}满足an+an+2=2an+1 ， 并写出数列{an}的通项公式；
（3）在（2）的条件下，设cn= 
， 求证：数列{cn}中的任意一项总可以表示成该数列其他两项之积．
【答案】
（1）解：因为数列{an}是首项为 
，公比为- 
的等比数列
所以 
， 
所以 
（2）解：若bn=n，则2Sn=（an+2）n，所以2Sn+1=（n+1）（an+1+2）
所以2an+1=（n+1）an+1﹣nan+2，即（n﹣1）an+1+2=nan
所以nan+2+2=（n+1）an+1
所以nan+2﹣（n﹣1）an+1=（n+1）an+1﹣nan
所以an+an+2=2an+1
又由2S1=a1+2，得：a1=2
所以数列{an}是首项为2公差为1的等差数列
所以an=n+1
（3）解：证明：由（2）知 
，
对于给定的n∈N*，若存在k，t≠n，且t，k∈N*，使得cn=ckct，
只需 
只需 
取k=n+1，则t=n（n+2）
所以对于数列{cn}中的任意一项 ，
都存在Cn+1= 
与Cn（n+2）= 
，使得cn=cn+1cn（n+2），
即数列{cn}中的任意一项总可以表示成该数列其他两项之积
【解析】（1）通过数列{an}是首项为 ，公比为- 的等比数列求出通项公式，然后求解 ．（2）若bn=n，通过an=Sn﹣Sn+1 ， 得到递推关系式，化简推出数列{an}是首项为2公差为1的等差数列，求出通项公式．（3）由（2）知 ，对于给定的n∈N* ， 若存在k，t≠n，且t，k∈N* ， 使得cn=ckct ， 证明 ，构造 ，然后证明数列{cn}中的任意一项总可以表示成该数列其他两项之积．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系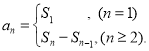
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
