题目内容
如图,从山脚下P处经过山腰N到山顶M拉一条电缆,PN的长为a米,NM的长为2a米,在P处测得M、N的仰角分别为45°,30°,在N处测得M的仰角为30°.(1)求此山的高度;
(2)试求平面PMN与水平面所成角的余弦值.

【答案】分析:(1)过M作MA垂直过P的水平面于A,过N作NB垂直过P的水平面于B,则MA∥NB,连接AB,PA,PM,PB,过N作NH⊥MA于H,可得:四凌锥P-ABNM的底面ABNM为直角梯形,从而可求山的高度;
(2)解法1:利用面积射影法,分别求得 ,
,
 ,从而可求平面PMN与水平面所成角的余弦值;
,从而可求平面PMN与水平面所成角的余弦值;
解法2:以A为原点AB、AM分别为y、z轴建立直角坐标系,求出平面MNP的一个法向量 ,水平面PAB的一个法向量
,水平面PAB的一个法向量 ,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值;
,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值;
解法3:设直线MN与AB交于点C,连PC,过B作BD垂直于PC于点D,连ND.则∠NDB为所求二面角的平面角,可求得 ,从而可得平面PMN与水平面所成角的余弦值.
,从而可得平面PMN与水平面所成角的余弦值.
解答:解:(1)如图,过M作MA垂直过P的水平面于A,过N作NB垂直过P的水平面于B,则MA∥NB
连接AB,PA,PM,PB,过N作NH⊥MA于H,
依题意得:四凌锥P-ABNM的底面ABNM为直角梯形,∠NPB=30°,∠MPB=45°,∠MNH=30°,
∴
山高 米
米
(2)
解法1:设平面PMN与水平面所成角为θ,则
△MNP中,
∴ ,
,
∵△APB为直角三角形,∴
∴
解法2:以A为原点AB、AM分别为y、z轴建立直角坐标系,不妨设a=1,则

设平面MNP的一个法向量 ,则
,则
即 令x=1,解得
令x=1,解得
又水平面PAB的一个法向量 ,
,
设平面PMN与水平面所成角为θ,则 =
= ,
,
∴平面PMN与水平面所成角的余弦值为 .
.
解法3:设直线MN与AB交于点C,连PC,过B作BD垂直于PC于点D,连ND.
则∠NDB为所求二面角的平面角
由MA∥NB, 得
得 ,
, ,
,
∴
∴平面PMN与水平面所成角的余弦值为 .
.
点评:本题主要考查空间线面关系、空间角、解三角形等基础知识;考查空间想象能力,考查运算求解能力以及分析问题解决问题的能力;考查数形结合、化归与转化等数学思想.
(2)解法1:利用面积射影法,分别求得
 ,
, ,从而可求平面PMN与水平面所成角的余弦值;
,从而可求平面PMN与水平面所成角的余弦值;解法2:以A为原点AB、AM分别为y、z轴建立直角坐标系,求出平面MNP的一个法向量
 ,水平面PAB的一个法向量
,水平面PAB的一个法向量 ,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值;
,利用向量的夹角公式,即可求得平面PMN与水平面所成角的余弦值;解法3:设直线MN与AB交于点C,连PC,过B作BD垂直于PC于点D,连ND.则∠NDB为所求二面角的平面角,可求得
 ,从而可得平面PMN与水平面所成角的余弦值.
,从而可得平面PMN与水平面所成角的余弦值.解答:解:(1)如图,过M作MA垂直过P的水平面于A,过N作NB垂直过P的水平面于B,则MA∥NB
连接AB,PA,PM,PB,过N作NH⊥MA于H,
依题意得:四凌锥P-ABNM的底面ABNM为直角梯形,∠NPB=30°,∠MPB=45°,∠MNH=30°,
∴

山高
 米
米 (2)

解法1:设平面PMN与水平面所成角为θ,则

△MNP中,

∴
 ,
,∵△APB为直角三角形,∴

∴

解法2:以A为原点AB、AM分别为y、z轴建立直角坐标系,不妨设a=1,则


设平面MNP的一个法向量
 ,则
,则
即
 令x=1,解得
令x=1,解得
又水平面PAB的一个法向量
 ,
,设平面PMN与水平面所成角为θ,则
 =
= ,
,∴平面PMN与水平面所成角的余弦值为
 .
.解法3:设直线MN与AB交于点C,连PC,过B作BD垂直于PC于点D,连ND.
则∠NDB为所求二面角的平面角
由MA∥NB,
 得
得 ,
, ,
,∴

∴平面PMN与水平面所成角的余弦值为
 .
.点评:本题主要考查空间线面关系、空间角、解三角形等基础知识;考查空间想象能力,考查运算求解能力以及分析问题解决问题的能力;考查数形结合、化归与转化等数学思想.

练习册系列答案
相关题目
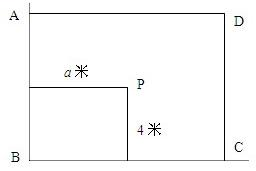
 在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.
在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程. 如图,从山脚下P处经过山腰N到山顶M拉一条电缆,PN的长为a米,NM的长为2a米,在P处测得M、N的仰角分别为45°,30°,在N处测得M的仰角为30°.
如图,从山脚下P处经过山腰N到山顶M拉一条电缆,PN的长为a米,NM的长为2a米,在P处测得M、N的仰角分别为45°,30°,在N处测得M的仰角为30°.