题目内容
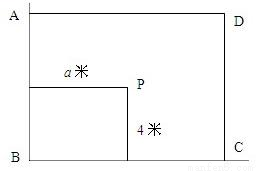
用长为16米的篱笆,借助墙角围成一个矩形ABCD(如图),在P处有一棵树与两墙的距离分别为a米(0<a<12)和4米.若此树不圈在矩形外,求矩形ABCD面积的最大值M.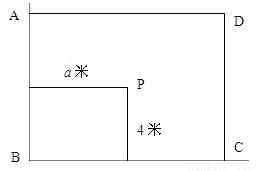
【答案】分析:先设AB=x,则AD=16-x,依题意建立不等关系得出x的取值范围,再写出SABCD=的函数解析式,下面分类讨论:(1)当16-a>8(2)当16-a≤8,分别求出矩形ABCD面积的面积值即可.
解答:解:设AB=x,则AD=16-x,依题意得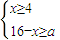 ,
,
即4≤x≤16-a(0<a<12)(2分)
SABCD=x(16-x)=64-(x-8)2.(6分)
(1)当16-a>8,即0<a<8时,
f(x)max=f(8)=64(10分)
(2)当16-a≤8,即8≤a<12时,
f(x)在[4,16-a]上是增函数,(14分)
∴f(x)max=f(16-a)=-a2+16a,
故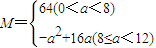 .(16分)
.(16分)
点评:构造二次函数模型,函数解析式求解是关键,然后利用配方法、数形结合法等方法求解二次函数最值,但要注意自变量的实际取值范围,本题求出的函数是分段函数的形式,在分段函数模型的构造中,自变量取值的分界是关键点,只有合理的分类,正确的求解才能成功地解题.
解答:解:设AB=x,则AD=16-x,依题意得
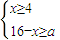 ,
,即4≤x≤16-a(0<a<12)(2分)
SABCD=x(16-x)=64-(x-8)2.(6分)
(1)当16-a>8,即0<a<8时,
f(x)max=f(8)=64(10分)
(2)当16-a≤8,即8≤a<12时,
f(x)在[4,16-a]上是增函数,(14分)
∴f(x)max=f(16-a)=-a2+16a,
故
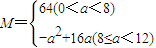 .(16分)
.(16分)点评:构造二次函数模型,函数解析式求解是关键,然后利用配方法、数形结合法等方法求解二次函数最值,但要注意自变量的实际取值范围,本题求出的函数是分段函数的形式,在分段函数模型的构造中,自变量取值的分界是关键点,只有合理的分类,正确的求解才能成功地解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
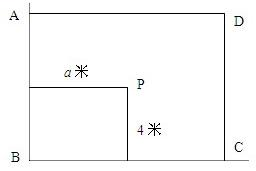
 用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).
用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).