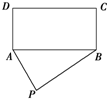
题目内容
 在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.
在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.分析:灾民区ABCD中的点可分为三类,第一类沿道路PA送药较近,第二类沿道路PB送药较近,第三类沿道路PA,PB送药一样远近,由题意可知,界线应该是第三类点的轨迹.建立坐标系,利用双曲线的定义,即可得到结论.
解答: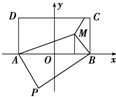 解:灾民区ABCD中的点可分为三类,第一类沿道路PA送药较近,第二类沿道路PB送药较近,第三类沿道路PA,PB送药一样远近,由题意可知,界线应该是第三类点的轨迹.
解:灾民区ABCD中的点可分为三类,第一类沿道路PA送药较近,第二类沿道路PB送药较近,第三类沿道路PA,PB送药一样远近,由题意可知,界线应该是第三类点的轨迹.
设M为界线上的任意一点,则有PA+MA=PB+MB,即MA-MB=PB-PA=50(定值),
∴界线为以A,B为焦点的双曲线的右支的一部分.
如图所示.以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,设所求双曲线的标准方程为
-
=1(a>0,b>0)
∵a=25,2c=AB=
=50
∴c=25
,b2=c2-a2=3750
∴双曲线方程为
-
=1
∵C(25
,70)
∴ymax=60,此时x=35,
∴所求方程为
-
=1(25≤x≤35,y>0).
 解:灾民区ABCD中的点可分为三类,第一类沿道路PA送药较近,第二类沿道路PB送药较近,第三类沿道路PA,PB送药一样远近,由题意可知,界线应该是第三类点的轨迹.
解:灾民区ABCD中的点可分为三类,第一类沿道路PA送药较近,第二类沿道路PB送药较近,第三类沿道路PA,PB送药一样远近,由题意可知,界线应该是第三类点的轨迹.设M为界线上的任意一点,则有PA+MA=PB+MB,即MA-MB=PB-PA=50(定值),
∴界线为以A,B为焦点的双曲线的右支的一部分.
如图所示.以AB所在直线为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,设所求双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵a=25,2c=AB=
| 1002+1502-2×100×150×cos60° |
| 7 |
∴c=25
| 7 |
∴双曲线方程为
| x2 |
| 625 |
| y2 |
| 3750 |
∵C(25
| 7 |
∴ymax=60,此时x=35,
∴所求方程为
| x2 |
| 625 |
| y2 |
| 3750 |
点评:本题考查双曲线的定义,考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
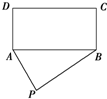 在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.
在抗震救灾行动中,某部队在如图所示的P处空降了一批救灾药品,急需把这批药品沿道路PA,PB送到矩形灾民区ABCD中去,已知PA=100km,PB=150km,BC=60km,∠APB=60°,试在灾民区确定一条界线,使位于界线一侧的点沿道路PA送药较近,而另一侧的点沿道路PB送药较近,请说明这一界线是一条什么曲线?并求出其方程.