Question

已知两圆C₁：x²＋y²－2x＋10y－24＝0，C₂：x²＋y²＋2x＋2y－8＝0，

(1)求两圆公共弦的长；

(2)求以公共弦为直径的圆的方程．

Answer 1

答案：
解析：

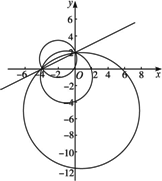
解：(1)画出如图示意图，两圆方程相减得x－2y＋4＝0，此即公共弦所在直线方程，又圆C2的圆心C2(－1，－1)到公共弦的距离d＝，且d2＋()2＝r22(l为公共弦长)， 　　∴l＝，即公共弦长为． 　　(2)解法一：连心线C1C2的方程为2x＋y＋3＝0， 它与公共弦的交点(－2，1)， 　　即为所求圆的圆心， 　　又所求圆半径为， 　　∴圆的方程为(x＋2)2＋(y－1)2＝5． 　　解法二：∵所求圆经过两圆交点， 　　设圆方程为(x2＋y2－2x＋10y－24)＋λ(x2＋y2＋2x＋2y－8)＝0， 　　即(1＋λ)x2＋(1＋λ)y2＋(2λ－2)x＋(2λ＋10)y－8λ－24＝0．① 　　其圆心为()． 　　∵圆心在公共弦x－2y＋4＝0上， 　　∴＋4＝0． 　　解得λ＝－3． 　　代入①并整理得，所求圆方程为x2＋y2＋4x－2y＝0． 　　思路分析：(1)先求出公共弦所在直线方程，再利用半径、圆心到直线距离、弦长之半构成的直角三角形求解； 　　(2)求出圆心、半径，也可用经过两圆交点的圆系方程求解．

提示：

解有关圆的问题，应充分利用圆的几何性质进行解题．借助圆的几何性质，减少不必要的计算．