题目内容
直线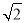 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0 B. C.
C. -1 D.
-1 D. +1
+1
C
【解析】根据题意画出图形,如图所示,

过点O作OC⊥AB于C,因为△AOB为等腰直角三角形,所以C为弦AB的中点,又|OA|=|OB|=1,根据勾股定理得|AB|= ,∴|OC|=
,∴|OC|= |AB|=
|AB|= .∴圆心到直线的距离为
.∴圆心到直线的距离为 =
= ,即2a2+b2=2,即a2=-
,即2a2+b2=2,即a2=- b2+1≥0.
b2+1≥0.
∴- ≤b≤
≤b≤ .则点P(a,b)与点(0,1)之间距离
.则点P(a,b)与点(0,1)之间距离
d= =
= =
= .
.
设f(b)= b2-2b+2=
b2-2b+2= (b-2)2,此函数为对称轴为x=2的开口向上的抛物线,∴当-
(b-2)2,此函数为对称轴为x=2的开口向上的抛物线,∴当- ≤b≤
≤b≤ <2时,函数为减函数.∵f(
<2时,函数为减函数.∵f( )=3-2
)=3-2 ,∴d的最小值为
,∴d的最小值为 =
= =
= -1.故C正确
-1.故C正确

练习册系列答案
相关题目











