题目内容
函数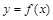 的图象如图所示,则导函数
的图象如图所示,则导函数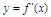 的图象可能是 ( )
的图象可能是 ( ) 
D
解析试题分析:先根据导函数f'(x)的图象得到f'(x)的取值范围,从而得到原函数的斜率的取值范围,从而得到正确选项.由于原函数都是递减区间可知导数都小于零,故排除A,B,C,只能选D.
考点:导数的几何意义
点评:题主要考查了导数的几何意义,同时考查了识图能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
曲线y=2sinx在点P(π,0)处的切线方程为 ( )
A.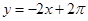 | B.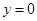 |
C.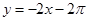 | D.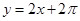 |
已知函数 满足
满足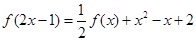 ,则函数
,则函数 在
在 处的切线是 ( )
处的切线是 ( )
A.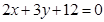 | B. |
C.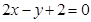 | D.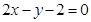 |
曲线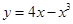 在点
在点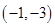 处的切线方程是( )
处的切线方程是( )
A.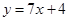 | B.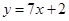 | C.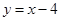 | D. |
设函数y=f(x),x∈R的导函数为 ,且
,且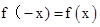 ,
, ,则下列成立的是( )
,则下列成立的是( )
| A.f(0)<e?1f(1)<e2f(2) | B.e2f(2)< f(0)<e?1f(1) |
| C.e2f(2)<e?1f(1)<f(0) | D.e?1f(1)<f(0)<e2f(2) |
函数f(x)=(x-3)ex的单调递增区间是( )
| A.(-∞,2) | B.(0,3) | C.(1,4) | D.(2,+∞) |
函数
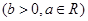 在点
在点 处的切线斜率的最小值是( )
处的切线斜率的最小值是( )
A. | B. | C. | D. |
设 ,曲线
,曲线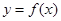 在点
在点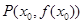 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为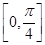 ,则点
,则点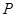 到曲线
到曲线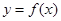 对称轴距离的取值范围是( )
对称轴距离的取值范围是( )
A. | B.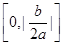 | C.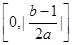 | D.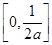 |
 为
为 ,那么,原油温度的瞬时变化率的最小值是( )
,那么,原油温度的瞬时变化率的最小值是( )

