题目内容
设函数y=f(x),x∈R的导函数为 ,且
,且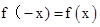 ,
, ,则下列成立的是( )
,则下列成立的是( )
| A.f(0)<e?1f(1)<e2f(2) | B.e2f(2)< f(0)<e?1f(1) |
| C.e2f(2)<e?1f(1)<f(0) | D.e?1f(1)<f(0)<e2f(2) |
D
解析试题分析:设 则
则 ,所以g(x)为减函数。
,所以g(x)为减函数。
因为,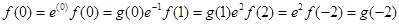 ,且g(-2)>g(0)>g(1),故选D。
,且g(-2)>g(0)>g(1),故选D。
考点:应用导数研究函数的单调性
点评:中档题,比较大小问题,往往应用函数的单调性,利用导数研究函数的单调性,是基本方法。本题关键是构造函数 。
。

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列求导正确的是
A.(x+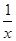 )’=1+ )’=1+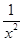 |
B.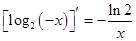 |
C.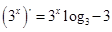 |
D.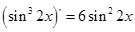 |
设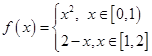 ,则
,则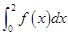 的值为( )
的值为( )
A.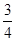 | B.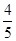 | C.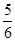 | D.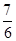 |
已知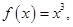 且
且 则
则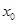 = ( )
= ( )
A. | B.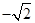 | C.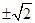 | D.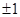 |
已知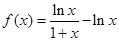 ,
, 在
在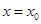 处取得最大值,以下各式中正确的序号为( )
处取得最大值,以下各式中正确的序号为( )
①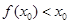 ②
②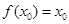 ③
③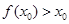 ④
④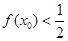 ⑤
⑤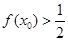
| A.①④ | B.②④ | C.②⑤ | D.③⑤ |
若曲线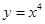 的一条切线l与直线
的一条切线l与直线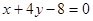 垂直,则l的方程为 ( )
垂直,则l的方程为 ( )
A.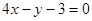 | B.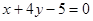 |
C.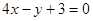 | D.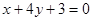 |
已知 是定义在
是定义在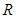 上的函数,若
上的函数,若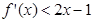 且
且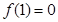 ,则
,则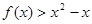 的解集为( )
的解集为( )
A.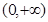 | B.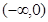 | C.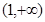 | D.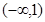 |
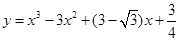 上移动,经过点P的切线的倾斜角为
上移动,经过点P的切线的倾斜角为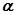 ,则角
,则角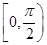
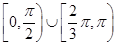


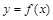 的图象如图所示,则导函数
的图象如图所示,则导函数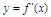 的图象可能是 ( )
的图象可能是 ( ) 