题目内容
20.已知关于x的方程x2+(1+a)x+1+a+b=0(a,b∈R)的两根分别为x1,x2且-1<x1<1<x2<2,则$\frac{b}{a}$的取值范围是(-$\frac{5}{4}$,1).分析 设f(x)=x2+(1+a)x+1+a+b,则由题意可得$\left\{\begin{array}{l}{f(1)=3+2a+b<0}\\{f(2)=7+3a+b>0}\\{f(-1)=1+b>0}\end{array}\right.$,利用简单的线性规划的知识求得目标函数z的范围.
解答  解:设f(x)=x2+(1+a)x+1+a+b,则由题意可得$\left\{\begin{array}{l}{f(1)=3+2a+b<0}\\{f(2)=7+3a+b>0}\\{f(-1)=1+b>0}\end{array}\right.$,
解:设f(x)=x2+(1+a)x+1+a+b,则由题意可得$\left\{\begin{array}{l}{f(1)=3+2a+b<0}\\{f(2)=7+3a+b>0}\\{f(-1)=1+b>0}\end{array}\right.$,
即 $\left\{\begin{array}{l}{2a+b<-3}\\{3a+b>-7}\\{b>-1}\end{array}\right.$,画出可行域,如图△ABC的内部区域,
则目标函数z=$\frac{b}{a}$表示可行域内的点(a,b),
与原点(0,0)连线的斜率.
求得A(-2,-1)、B(-1,-1)、C(-4,5),
故0≥$\frac{b}{a}$>KOC,或0≤$\frac{b}{a}$<KOB,
即 0≥$\frac{b}{a}$>-$\frac{5}{4}$,或0≤$\frac{b}{a}$<1,
故答案为:(-$\frac{5}{4}$,1).
点评 本题主要考查一元二次方程根的分布与系数的关系,简单的线性规划,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
11. 已知函数f(x)=x|x-m|,x∈R.且f(4)=0
已知函数f(x)=x|x-m|,x∈R.且f(4)=0
(1)求实数m的值.
(2)作出函数f(x)的图象,并根据图象写出f(x)的单调区间
(3)若方程f(x)=k有三个实数解,求实数k的取值范围.
 已知函数f(x)=x|x-m|,x∈R.且f(4)=0
已知函数f(x)=x|x-m|,x∈R.且f(4)=0(1)求实数m的值.
(2)作出函数f(x)的图象,并根据图象写出f(x)的单调区间
(3)若方程f(x)=k有三个实数解,求实数k的取值范围.
15.若$\sqrt{\frac{1-sinx}{1+sinx}}$=$\frac{sinx-1}{cosx}$,则x的取值范围是( )
| A. | 2kπ≤x≤2kπ+$\frac{π}{2}$,k∈Z | B. | 2kπ+$\frac{π}{2}$<x<2kπ+$\frac{3π}{2}$,k∈Z | ||
| C. | 2kπ+$\frac{3π}{2}$<x<2kπ+2π,k∈Z | D. | 2kπ+π<x<2kπ+$\frac{3π}{2}$,k∈Z |
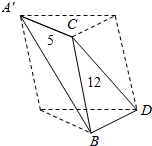 将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.
将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.