题目内容
12.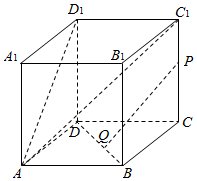 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,满足PQ∥平面AC1D1,则PQ与平面BDD1B1所成角的范围是($\frac{π}{6}$,$\frac{π}{3}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P,Q分别是线段CC1,BD上的点,满足PQ∥平面AC1D1,则PQ与平面BDD1B1所成角的范围是($\frac{π}{6}$,$\frac{π}{3}$].
分析 :以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出PQ与平面BDD1B1所成角的范围.
解答 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系
则A(1,0,0),C1(0,1,1),D1(0,0,1),
$\overrightarrow{A{D}_{1}}$=(-1,0,1),$\overrightarrow{A{C}_{1}}$=(-1,1,1),
设平面AC1D1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{D}_{1}}=-x+z=0}\\{\overrightarrow{n}•\overrightarrow{A{C}_{1}}=-x+y+z=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
设P(0,1,t),Q(a,b,0),a,b,t∈[0,1),$\overrightarrow{DQ}=λ\overrightarrow{DB}$,0≤λ<1,
∴(a,b,0)=(λ,λ,0),∴Q(λ,λ,0),$\overrightarrow{PQ}=(λ,λ-1,-t)$,
∵PQ∥平面AC1D1,∴$\overrightarrow{PQ}•\overrightarrow{n}=λ-t=0$,t=λ,∴$\overrightarrow{PQ}=(λ,λ,-λ)$,
∵AC⊥平面BDD1B1,∴平面BDD1B1的一个法向量$\overrightarrow{AC}$=(-1,1,0),
设PQ与平面BDD1B1所成角为θ,
则sinθ=|cos<$\overrightarrow{PQ},\overrightarrow{AC}$>|=|$\frac{\overrightarrow{PQ}•\overrightarrow{AC}}{|\overrightarrow{PQ}|•|\overrightarrow{AC}|}$|
=$\frac{1}{\sqrt{2}•\sqrt{3{λ}^{2}-2λ+1}}$=$\frac{1}{\sqrt{2}•\sqrt{3(λ-\frac{1}{3})^{2}+\frac{2}{3}}}$,0≤λ<1,
∴λ=$\frac{1}{3}$时,(sinθ)max=$\frac{1}{\sqrt{2}•\sqrt{\frac{2}{3}}}$=$\frac{\sqrt{3}}{2}$,此时$θ=\frac{π}{3}$,
λ=1时,(sinθ)min=$\frac{1}{\sqrt{2}•\sqrt{2}}$=$\frac{1}{2}$,此时$θ=\frac{π}{6}$,
∴PQ与平面BDD1B1所成角的范围是($\frac{π}{6}$,$\frac{π}{3}$].
故答案为:$(\frac{π}{6},\frac{π}{3}]$.
点评 本题考查直线与平面所成角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
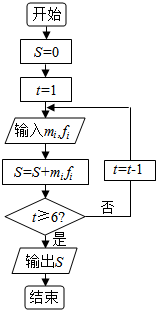 “世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图.
“世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图. | 序号 (i) | 分组 睡眠时间 | 组中值 (mi) | 频数 (人数) | 频率 (fi) |
| 1 | [4,5) | 4.5 | 8 | 0.04 |
| 2 | [5,6) | 5.5 | 52 | 0.26 |
| 3 | [6,7) | 6.5 | m | 0.30 |
| 4 | [7,8) | 7.5 | 56 | 0.28 |
| 5 | [8,9) | 8.5 | 20 | n |
| 6 | [9,10] | 9.5 | 4 | 0.02 |
(2)求输出S的值
(3)S的统计意义是什么?
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 根据样本估计总体,其误差与所选择的样本容量无关 | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |