题目内容
某大楼共有12层，有11人在第1层上了电梯，他们分别要去第2至第12层，每层1人．因特殊原因，电梯只允许停1次，只可使1人如愿到达，其余10人都要步行到达所去的楼层．假设这10位乘客的初始“不满意度”均为0，乘客每向下步行1层的“不满意度”增量为1，每向上步行1层的“不满意度”增量为2，10人的“不满意度”之和记为S，则S的最小值是（ ）A．42
B．41
C．40
D．39
【答案】分析：先设电梯停在第x层，根据条件找到S和x的函数关系，再利用开口向上的二次函数最小值求法，求出x的值即可．
解答：解：设电梯停在第x层，则向下走的有（x-2）人，向上走的有（12-x）人，
有题得 S=[1+2+3+…+（x-2）]+2[1+2+3+…+（12-x）]
=
+2×
=
．
开口向上，对称轴为x=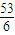
≈9，
故S在x=9时取最小值Smin=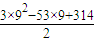
=40．
故选C．
点评：本题是等差数列的求和公式在实际生活中的应用，体现了数学服务于生活的特点．是中墚题．
解答：解：设电梯停在第x层，则向下走的有（x-2）人，向上走的有（12-x）人，
有题得 S=[1+2+3+…+（x-2）]+2[1+2+3+…+（12-x）]
=
+2×=．开口向上，对称轴为x=
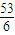≈9，故S在x=9时取最小值Smin=
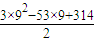=40．故选C．
点评：本题是等差数列的求和公式在实际生活中的应用，体现了数学服务于生活的特点．是中墚题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
相关题目