题目内容
点P(x0,y0)是曲线C:y=
(x>0)上的一个动点,曲线C在点P处的切线与x轴、y周分别交于A,B两点,点O是坐标原点.给出三个命题:①PA=PB;②△OAB的面积为定值;③曲线C上存在两点M,N,使得△OMN为等腰直角三角形.其中真命题的个数是
| 1 | x |
3
3
.分析:曲线C在点P处的切线方程为
+y-
=0,求出A(2x0,0),B(0,
),P(x0,
),由此得到PA=PB,△OAB的面积S=
×2x0×
=2;由题意知曲线C上存在两点M,N,使得△OMN为等腰直角三角形.
| x |
| x02 |
| 2 |
| x0 |
| 2 |
| x0 |
| 1 |
| x0 |
| 1 |
| 2 |
| 2 |
| x0 |
解答:解:∵y=
(x>0),
∴y′=-
,
∴曲线C在点P处的切线方程为:y-
=-
(x-x0),
整理,得
+y-
=0,
∴A(2x0,0),B(0,
),P(x0,
),
∴PA=PB=
,故①正确;
∵A(2x0,0),B(0,
),
∴△OAB的面积S=
×2x0×
=2,故②正确;
mo=mn并且mo垂直于mn时,曲线C上存在两点M,N,使得△OMN为等腰直角三角形,故③正确.
故答案为:3.
| 1 |
| x |
∴y′=-
| 1 |
| x2 |
∴曲线C在点P处的切线方程为:y-
| 1 |
| x0 |
| 1 |
| x02 |
整理,得
| x |
| x02 |
| 2 |
| x0 |
∴A(2x0,0),B(0,
| 2 |
| x0 |
| 1 |
| x0 |
∴PA=PB=
x02+
|
∵A(2x0,0),B(0,
| 2 |
| x0 |
∴△OAB的面积S=
| 1 |
| 2 |
| 2 |
| x0 |
mo=mn并且mo垂直于mn时,曲线C上存在两点M,N,使得△OMN为等腰直角三角形,故③正确.
故答案为:3.
点评:本题考查反比例函数的性质和应用,解题时要认真审题,注意导数的性质的灵活运用.

练习册系列答案
相关题目
 已知椭圆
已知椭圆 已知抛物线x2=2py(p>0)上的一点(m,1)到焦点的距离为
已知抛物线x2=2py(p>0)上的一点(m,1)到焦点的距离为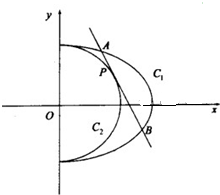 (2013•济宁一模)如图,已知半椭圆C1:
(2013•济宁一模)如图,已知半椭圆C1: