题目内容
 已知抛物线x2=2py(p>0)上的一点(m,1)到焦点的距离为
已知抛物线x2=2py(p>0)上的一点(m,1)到焦点的距离为| 5 | 4 |
(I)求抛物线的方程;
(II)求证:点P′在y轴上.
分析:(Ⅰ)由抛物线的定义可得 1+
p=
,可求抛物线的方程
(II)设P1(x1,y1),P2(x2,y2)由导数的几何意义可求以点P1为切点的抛物线的切线方程为y-y1=2x1(x-x1),结合y1=x12,可得y=2x1x-x12,P2为切点的抛物线的切线方程为y=2x2x-x22,从而可求P′,由直线PM1的方程及抛物线方程可求y=
x-1则由方程的根与系数关系可得,x1=
,同理可得x2=-
可证
| 1 |
| 2 |
| 5 |
| 4 |
(II)设P1(x1,y1),P2(x2,y2)由导数的几何意义可求以点P1为切点的抛物线的切线方程为y-y1=2x1(x-x1),结合y1=x12,可得y=2x1x-x12,P2为切点的抛物线的切线方程为y=2x2x-x22,从而可求P′,由直线PM1的方程及抛物线方程可求y=
| y0+1 |
| x0 |
| 1 |
| x0 |
| 1 |
| x0 |
解答:(Ⅰ)解:由题意得 1+
p=
,
∴p=
所以抛物线的方程为y=x2…(6分)
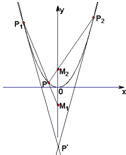
(II)证明:设P1(x1,y1),P2(x2,y2)因为y′=2x
则以点P1为切点的抛物线的切线方程为
y-y1=2x1(x-x1) 又y1=x12,所以y=2x1x-x12…(9分)
同理可得以点P2为切点的抛物线的切线方程为y=2x2x-x22
由
解得x=
…(11分)
又过点P(x0,y0)与M1(0,-1)的直线的斜率为k1=
所以直线PM1的方程为y=
x-1
由
得x2-
x+1=0
所x0x1=1,即x1=
…(13分)
同理可得直线PM2的方程y=
x+1
由
得 x2-
x-1=0
所以x0x2=-1,即x2=-
则x1+x2=
+(-
)=0,即P′得横坐标为0,
所以点P′在y轴上…(15分)
| 1 |
| 2 |
| 5 |
| 4 |
∴p=
| 1 |
| 2 |
所以抛物线的方程为y=x2…(6分)
(II)证明:设P1(x1,y1),P2(x2,y2)因为y′=2x
则以点P1为切点的抛物线的切线方程为
y-y1=2x1(x-x1) 又y1=x12,所以y=2x1x-x12…(9分)
同理可得以点P2为切点的抛物线的切线方程为y=2x2x-x22
由
|
| x1+x2 |
| 2 |
又过点P(x0,y0)与M1(0,-1)的直线的斜率为k1=
| y0+1 |
| x0 |
所以直线PM1的方程为y=
| y0+1 |
| x0 |
由
|
| y0+1 |
| x0 |
所x0x1=1,即x1=
| 1 |
| x0 |
同理可得直线PM2的方程y=
| y0-1 |
| x0 |
由
|
| y0-1 |
| x0 |
所以x0x2=-1,即x2=-
| 1 |
| x0 |
则x1+x2=
| 1 |
| x0 |
| 1 |
| x0 |
所以点P′在y轴上…(15分)
点评:本题主要考查了利用抛物线的性质求解抛物线的方程,直线与抛物线相交关系的应用,导数的几何意义的应用,属于综合试题

练习册系列答案
相关题目
 (2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2
(2011•合肥三模)已知抛物线C的方程为x2=2py(p>0),过抛物线上点M(-2