题目内容
(2006•广州一模)已知sin
-cos
=
,α∈(
,π),tanβ=
.
(Ⅰ)求sinα的值;
(Ⅱ)求tan(α-β)的值.
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
| π |
| 2 |
| 1 |
| 2 |
(Ⅰ)求sinα的值;
(Ⅱ)求tan(α-β)的值.
分析:(Ⅰ)把已知等式sin
-cos
=
左右两边平方,利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可求出sinα的值;
(Ⅱ)由sinα及α的范围,利用同角三角函数间的基本关系求出cosα的值,再利用基本关系求出tanα的值,利用两角和与差的正切函数公式化简tan(α-β),将tanα及tanβ的值代入即可求出tan(α-β)的值.
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
(Ⅱ)由sinα及α的范围,利用同角三角函数间的基本关系求出cosα的值,再利用基本关系求出tanα的值,利用两角和与差的正切函数公式化简tan(α-β),将tanα及tanβ的值代入即可求出tan(α-β)的值.
解答:解:(Ⅰ)等式sin
-cos
=
左右两边平方得:
(sin
-cos
)2=sin2
+cos2
-2sin
cos
=1-sinα=(
)2=
,
∴sinα=
;
(Ⅱ)∵sinα=
,α∈(
,π),
∴cosα=-
=-
,
∴tanα=
=-
,又tanβ=
,
∴tan(α-β)=
=
=-
.
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
(sin
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
| ||
| 5 |
| 1 |
| 5 |
∴sinα=
| 4 |
| 5 |
(Ⅱ)∵sinα=
| 4 |
| 5 |
| π |
| 2 |
∴cosα=-
| 1-sin2α |
| 3 |
| 5 |
∴tanα=
| sinα |
| cosα |
| 4 |
| 3 |
| 1 |
| 2 |
∴tan(α-β)=
| tanα-tanβ |
| 1+tanαtanβ |
-
| ||||
1+(-
|
| 11 |
| 2 |
点评:此题考查了两角和与差的正切函数公式,同角三角函数间的基本关系,以及二倍角的正弦函数公式,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
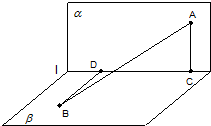 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,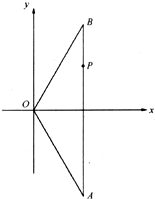 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.