题目内容
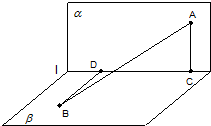 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,且AB与平面α、β所成的角都是30°,AC⊥l,垂足为C,BD⊥l,垂足为D.
(Ⅰ)求直线AB与CD所成角的大小;
(Ⅱ)求二面角C-AB-D所成平面角的余弦值.
分析:(Ⅰ)直接根据AC⊥β以及常用的结论:cosθ=cos∠ABC•cos∠DCB即可求出结果;
(Ⅱ)先建立空间直角坐标系,得到各对应点的坐标,进而求出两个平面的法向量的坐标,最后代入向量夹角计算公式即可.
(Ⅱ)先建立空间直角坐标系,得到各对应点的坐标,进而求出两个平面的法向量的坐标,最后代入向量夹角计算公式即可.
解答: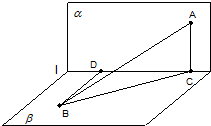 解:(Ⅰ)如图所示,连接BC,设直线AB与CD所成的角为θ,则由AC⊥β知:cosθ=cos∠ABC•cos∠DCB=cos30°•
解:(Ⅰ)如图所示,连接BC,设直线AB与CD所成的角为θ,则由AC⊥β知:cosθ=cos∠ABC•cos∠DCB=cos30°•
=
,
故θ=45°;
(Ⅱ)如图建立空间直角坐标系,则D(0,0,0),A(0,
,1),B(1,0,0),C(0,
,0),
所以
=(0,0,1),
=(1,-
,0),设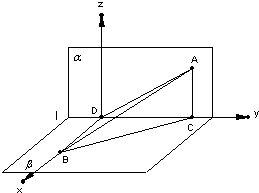
=(x,y,z)是平面ABC的法向量,则
⇒可以取
=(
,1,0).
同理,
=(0,1,-
)是平面ABD的法向量.
设二面角C-AB-D所成的平面角为γ,则显然γ是锐角,从而有cosγ=|
|=
=
.
 解:(Ⅰ)如图所示,连接BC,设直线AB与CD所成的角为θ,则由AC⊥β知:cosθ=cos∠ABC•cos∠DCB=cos30°•
解:(Ⅰ)如图所示,连接BC,设直线AB与CD所成的角为θ,则由AC⊥β知:cosθ=cos∠ABC•cos∠DCB=cos30°•
| ||
|
| ||
| 2 |
故θ=45°;
(Ⅱ)如图建立空间直角坐标系,则D(0,0,0),A(0,
| 2 |
| 2 |
所以
| CA |
| CB |
| 2 |

| n1 |
|
| n1 |
| 2 |
同理,
| n2 |
| 2 |
设二面角C-AB-D所成的平面角为γ,则显然γ是锐角,从而有cosγ=|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 3 |
点评:本小题主要考查空间直线所成的角以及二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.用空间向量求二面角问题的关键在于求出两个平面的法向量.

练习册系列答案
相关题目
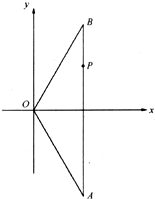 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.