题目内容
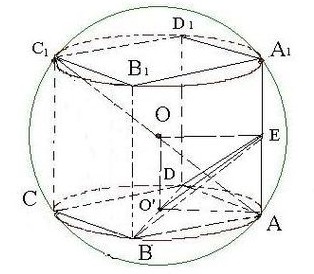
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8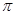 B.16
B.16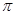 : C.14
: C.14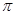 D.18
D.18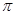
【答案】
B.
【解析】
试题分析:∵长方体ABCD—A1B1ClD1内接于球O,∴球心O是A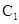 中点。
中点。
∵ABCD是边长为2的正方形,∴BD=2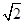 ,
,
设BD中点为O‘,连接OO'
∴OO'⊥平面ABCD
∵E为A 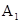 的中点,
的中点,
∴AE//OO', AE=OO'
∴AO'OE为矩形
∵OA垂直平面BDE
∴OA⊥EO'
∴AO'OE为正方形
∴AO=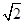 AO'=2
AO'=2
即球O的半径R=2
∴球O面积4πR²=16π,故选B。
考点:本题主要考查立体几何平行关系、垂直关系、长方体、球的几何特征,球的表面积计算。
点评:中档题,首先认定球心O是A 中点,围绕球半径的计算,构造出现直角三角形,利用直角三角形的边角关系求解。
中点,围绕球半径的计算,构造出现直角三角形,利用直角三角形的边角关系求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点.
已知长方体ABCD-A1B1C1D1中,AB=2,BC=4,AA1=4,点M是棱D1C1的中点. 已知长方体ABCD-A1B1C1D1中,DA=DD1=1,
已知长方体ABCD-A1B1C1D1中,DA=DD1=1, 已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2,
已知长方体ABCD-A1B1C1D1中,M、N分别是BB1和BC的中点,AB=4,AD=2, 如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.
如图,已知长方体ABCD-A1B1C1D1,AB=BC=1,BB1=2,连接B1C,过B点作B1C.