题目内容
在平面直角坐标系中,若不等式组
表示一个三角形区域,则实数k的取值范围是( )
|
分析:根据直线方程的点斜式,得不等式y≤k(x-1)-1表示的平面区域为经过点M(-1,1)的直线l及其下方的平面区域.由此作出题中不等式组表示的平面区域,得到如图的△OAB及其内部.再观察直线AB的斜率变化,建立k的不等式即可得到实数k的取值范围.
解答:解:∵直线y=k(x-1)-1表示经过定点M(1,-1),且斜率为k的直线
∴不等式y≤k(x-1)-1表示的平面区域为经过点M的直线l及其下方的平面区域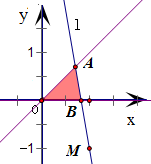
因此,作出不等式组
表示的平面区域,
得到如图的△OAB及其内部
因为该区域表示直线y=k(x-1)-1下方、直线y=x下方且在y=0的上方
所以直线AB的斜率k小于0,且点A位于直线y=x上原点O以上部分
∵OM的斜率为-1,∴k<-1
由此可得实数k的取值范围是(-∞,-1)
故答案为:(-∞,-1)
∴不等式y≤k(x-1)-1表示的平面区域为经过点M的直线l及其下方的平面区域

因此,作出不等式组
|
得到如图的△OAB及其内部
因为该区域表示直线y=k(x-1)-1下方、直线y=x下方且在y=0的上方
所以直线AB的斜率k小于0,且点A位于直线y=x上原点O以上部分
∵OM的斜率为-1,∴k<-1
由此可得实数k的取值范围是(-∞,-1)
故答案为:(-∞,-1)
点评:本题给出二元一次不等式组,当不等式组表示一个三角形平面区域时,求实数k的取值范围.着重考查了二元一次不等式组表示的平面区域和直线的斜率等知识,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目