题目内容
7.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=6,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{4}$,求$\overrightarrow{a}$•$\overrightarrow{b}$.分析 直接根据向量的夹角公式cos<$\overrightarrow{a}$•$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$,求得$\overrightarrow{a}$•$\overrightarrow{b}$.
解答 解:根据向量的夹角公式,
cos<$\overrightarrow{a}$•$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$得,
cos$\frac{π}{4}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{4×6}$=$\frac{\sqrt{2}}{2}$,
所以,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{\sqrt{2}}{2}$×24=12$\sqrt{2}$,
即$\overrightarrow{a}$•$\overrightarrow{b}$=12$\sqrt{2}$.
点评 本题主要考查了平面向量数量积的运算,向量的夹角公式,属于基础题.

练习册系列答案
相关题目
17.根据表,能够判断方程f(x)=g(x)在四个区间:①(-1,0);②(0,1);③(1,2);④(2,3)中有实数解的是②.(将正确的序号都填上)
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.6 | 3.1 | 5.4 | 5.9 | 7 |
| g(x) | -0.5 | 3.4 | 4.8 | 5.2 | 6 |
16.已知直线y=x-b与曲线C:y=$\sqrt{1-{x}^{2}}$-1有唯一交点,则b的取值范围是( )
| A. | {-$\sqrt{2}$-1,$\sqrt{2}$-1} | B. | {-$\sqrt{2}$+1,$\sqrt{2}$+1} | C. | [-2,0] | D. | (0,2]∪{1-$\sqrt{2}$} |
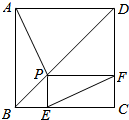 如图所示,P是正方形ABCD对角线BD上一点,四边形PECF是矩形,求证:
如图所示,P是正方形ABCD对角线BD上一点,四边形PECF是矩形,求证: