题目内容
【题目】已知椭圆E: ![]() =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ![]() ),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|=
),左右焦点为F1、F2 , 右顶点为A,上顶点为B,且|AB|= ![]() |F1F2|.
|F1F2|.
(1)求椭圆E的方程;
(2)直线l:y=﹣x+m与椭圆E交于C、D两点,与以F1、F2为直径的圆交于M、N两点,且 ![]() =
= ![]() ,求m的值.
,求m的值.
【答案】
(1)解:椭圆E: ![]() =1(a>b>0)焦点在x轴上,
=1(a>b>0)焦点在x轴上,
∵椭圆E过点 ![]() ,
,
∴将点(1, ![]() ),代入椭圆方程得
),代入椭圆方程得 ![]() ,①
,①
由已知 ![]() ,
,
∴ ![]() ,即a2+b2=7c2②
,即a2+b2=7c2②
又∵c2=a2﹣b2③,
将①②③联立得 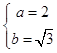 ,
,
∴椭圆方程为 ![]()
(2)解:根据题意,以F1、F2为直径的圆方程为x2+y2=1,
所以圆心(0,0)到直线l的距离为 ![]() ,所以|MN|=
,所以|MN|= ![]() ,
,
设C(x1,y1),D(x1,y1),联立  ,
,
化简得7x2﹣8mx+4m2﹣12=0,△=48(7﹣m2)>0,
![]() ,
, ![]()
由丨CD丨= ![]()
![]() ,
,
∴  =
= ![]() ,
,
由 ![]() 得
得 ![]() ,
,
整理得 ![]() ,即
,即 ![]() ,
,
经检验,当 ![]() 时,△=112(7﹣m2)>0成立,
时,△=112(7﹣m2)>0成立,
∴ ![]()
【解析】(1)由题意可知:椭圆焦点在x轴上,将点(1, ![]() )代入椭圆方程
)代入椭圆方程 ![]() ,由
,由 ![]() ,c2=a2﹣b2 , 联立即可求得a和b的值,即可求得椭圆E的方程;(2)圆心(0,0)到直线l的距离为
,c2=a2﹣b2 , 联立即可求得a和b的值,即可求得椭圆E的方程;(2)圆心(0,0)到直线l的距离为 ![]() ,所以|MN|=
,所以|MN|= ![]() ,将直线方程方程代入椭圆方程,由韦达定理及弦长公式可知:|CD|=
,将直线方程方程代入椭圆方程,由韦达定理及弦长公式可知:|CD|= ![]() ,由
,由 ![]() 得
得 ![]() ,整理即可求得m的值.
,整理即可求得m的值.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】某市政府为了实施政府绩效管理、创新政府公共服务模式、提高公共服务效率.实施了“政府承诺,等你打分”民意调查活动,通过问卷调查了学生、在职人员、退休人员共250人,统计结果表不幸被污损,如表:
学生 | 在职人员 | 退休人员 | |
满意 |
|
| 78 |
不满意 | 5 |
| 12 |
若在所调查人员中随机抽取1人,恰好抽到学生的概率为0.32.
(1)求满意学生的人数;
(2)现用分层抽样的方法在所调查的人员中抽取25人,则在职人员应抽取多少人?
(3)若满意的在职人员为77,则从问卷调查中填写不满意的“学生和在职人员”中选出2人进行访谈,求这2人中包含了两类人员的概率.
