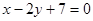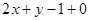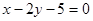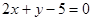题目内容
(本小题满分12分) 已知椭圆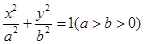 的离心率
的离心率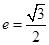 ,焦点到椭圆上的点的最短距离为
,焦点到椭圆上的点的最短距离为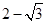 .
.
(I)求椭圆的标准方程.
(Ⅱ)设直线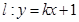 与椭圆交与M,N两点,当
与椭圆交与M,N两点,当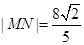 时,求直线
时,求直线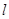 的方程.
的方程.
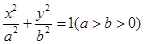 的离心率
的离心率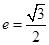 ,焦点到椭圆上的点的最短距离为
,焦点到椭圆上的点的最短距离为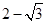 .
.(I)求椭圆的标准方程.
(Ⅱ)设直线
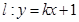 与椭圆交与M,N两点,当
与椭圆交与M,N两点,当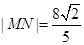 时,求直线
时,求直线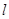 的方程.
的方程.(1) ;(2)
;(2) 。
。
 ;(2)
;(2) 。
。(I)由e可得 ,又因为
,又因为 ,所以可解得a,c的值,再利用
,所以可解得a,c的值,再利用
 求出
求出 ,从而确定椭圆的标准方程.
,从而确定椭圆的标准方程.
(II)在(1)的基础上,直线方程与椭圆方程联立消去y,得到关于x的一元二次方程,再借助韦达定理和弦长公式可建立关于k的方程.从而解出k值,确定l的方程.
解:(1)由已知得 解之得
解之得 …………2分
…………2分
则椭圆的标准方程为 …………4分
…………4分
(2)设 由
由 得
得 ………6分
………6分
 ………8分
………8分
 ………10分
………10分
解之得: ………11分
………11分
则直线方程为 ………12分
………12分
 ,又因为
,又因为 ,所以可解得a,c的值,再利用
,所以可解得a,c的值,再利用 求出
求出 ,从而确定椭圆的标准方程.
,从而确定椭圆的标准方程.(II)在(1)的基础上,直线方程与椭圆方程联立消去y,得到关于x的一元二次方程,再借助韦达定理和弦长公式可建立关于k的方程.从而解出k值,确定l的方程.
解:(1)由已知得
 解之得
解之得 …………2分
…………2分则椭圆的标准方程为
 …………4分
…………4分(2)设
 由
由 得
得 ………6分
………6分 ………8分
………8分 ………10分
………10分解之得:
 ………11分
………11分 则直线方程为
 ………12分
………12分
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
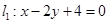 与
与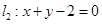 的交点为P,直
的交点为P,直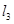 的方程为:
的方程为: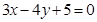 .
.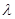 +1)x+(
+1)x+(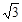 ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°];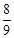 .
. 与直线
与直线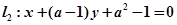 平行,则实数
平行,则实数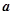 的值是( )
的值是( )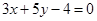 和直线
和直线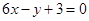 的交点,且与直线
的交点,且与直线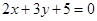 平行,则直线l的方程为 .
平行,则直线l的方程为 .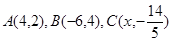 三点共线,则实数
三点共线,则实数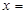 _________.
_________.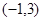 且平行于直线
且平行于直线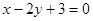 的直线方程为( ).
的直线方程为( ).