题目内容
以点(-2,3)为圆心且与y轴相切的圆的方程是 .
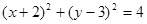
解析试题分析:圆心C的坐标为(-2,3),且所求圆与y轴相切,
∴圆的半径r=|-2|=2,
则所求圆的方程为(x+2)2+(y-3)2=4.
故答案为:(x+2)2+(y-3)2=4
考点:本题主要是考查直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,当直线与圆相切时,圆心到直线的距离等于圆的半径,
点评:解决该试题的关键是其中根据题意得到圆心横坐标的绝对值为圆的半径.要求圆的方程,注意找出圆心和半径,而圆心已知,故要求圆的半径,方法为:由所求圆与y轴相切,得到圆心的横坐标的绝对值为圆的半径,进而由圆心C的坐标和求出的半径写出圆的标准方程即可.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 平分圆
平分圆 的面积,且直线
的面积,且直线 与圆
与圆 相切,则
相切,则 .
. 上有且只有两个不同点到直线
上有且只有两个不同点到直线 :
: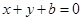 的距离为1,则
的距离为1,则 的取值范围是_________.
的取值范围是_________.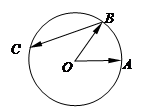
 上的点到直线
上的点到直线 的最小距离是 .
的最小距离是 .  的极坐标方程为
的极坐标方程为 ,则圆
,则圆
 的最短距离为 .
的最短距离为 .