题目内容
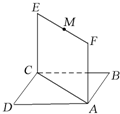 (2010•烟台一模)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
(2010•烟台一模)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
(1)求证AM∥平面BDE;
(2)试在线段AC上确定一点P,使得PF与CD所成的角是60°.
分析:(1)由题意建立空间直角坐标系,利用向量平行得到线线平行,从而说明线面平行;
(2)设出线段AC上P点的坐标,由PF与CD所成的角是60°,得到向量
与
所成的角的余弦值的绝对值等于
,由此可求得P点的坐标.
(2)设出线段AC上P点的坐标,由PF与CD所成的角是60°,得到向量
| PF |
| CD |
| 1 |
| 2 |
解答:(1)证明:如图建立空间直角坐标系.设AC∩BD=N,
连结NE,则N(
,
,0),E(0,0,1)∴
=(-
,-
,1)
又A(
,
,0),M(
,
,1),
∴
=(-
,-
,1).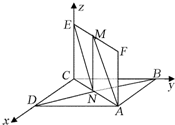
∴
=
,且NE与AM不共线,
∴NE∥AM,又NE?平面BDE,AM?平面BDE,
∴AM∥平面BDE.
(2)设P(t,t,0)(0≤t≤
),
则
=(
-t,
-t,1),
=(
,0,0).
又∵
与
所成的角为60°,∴
=
,
解之得t=
或t=
(舍去),
故点P为AC的中点时满足题意.
连结NE,则N(
| ||
| 2 |
| ||
| 2 |
| NE |
| ||
| 2 |
| ||
| 2 |
又A(
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AM |
| ||
| 2 |
| ||
| 2 |

∴
| NE |
| AM |
∴NE∥AM,又NE?平面BDE,AM?平面BDE,
∴AM∥平面BDE.
(2)设P(t,t,0)(0≤t≤
| 2 |
则
| PF |
| 2 |
| 2 |
| CD |
| 2 |
又∵
| PF |
| CD |
|(
| ||||||||
|
| 1 |
| 2 |
解之得t=
| ||
| 2 |
3
| ||
| 2 |
故点P为AC的中点时满足题意.
点评:本题考查了直线与平面平行的判定,考查了直线与直线所成角的求法,解答的关键是建立正确的右手系,利用向量证明线面平行时,最后要回归到直线与平面平行,是中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目