Question

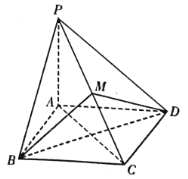
【题目】已知四棱锥P－ABCD的三视图如下图所示，E是侧棱PC上的动点．

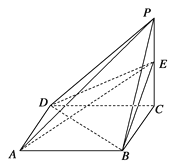
（1）求证：BD⊥AE

（2）若点E为PC的中点，求二面角D－AE－B的大小.

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题（1）要证明线线垂直，先证明线面垂直，所以观察几何体，先证明平面,而要证明线面垂直，先证明线与平面内的两条相交直线垂直，即证明,;

（2）法一，几何法，观察,所以可选择在平面DAE内过点D作DF⊥AE于F，连结BF，∠DFB为二面角D－AE－B的平面角，或法二，采用空间向量的方法，以点C为原点，CD，CB，CP所在的直线分别为x，y，z轴建立空间直角坐标系，分别求两个平面的法向量，或.

试题解析：（1）由三视图可知，四棱锥P－ABCD的底面是边长为1的正方形，

侧棱PC⊥底面ABCD，且PC＝2.

连结AC，∵ABCD是正方形， ∴BD⊥AC.

∵PC⊥底面ABCD，且BD平面ABCD， ∴BD⊥PC.

又∵AC∩PC＝C，∴BD⊥平面PAC.

∵AE平面PAC. ∴BD⊥AE.

（2）解法1：在平面DAE内过点D作DF⊥AE于F，连结BF.

∵AD＝AB＝1，DE＝BE＝，AE＝AE＝，

∴Rt△ADE≌Rt△ABE，

从而△ADF≌△ABF，∴BF⊥AE.

∴∠DFB为二面角D－AE－B的平面角．

在Rt△ADE中，DF＝， ∴.

又BD＝，在△DFB中，由余弦定理得

cos∠DFB＝，

∴∠DFB＝，即二面角D－AE－B的大小为

解法2：如图，以点C为原点，CD，CB，CP所在的直线分别为x，y，z轴建立空间直角坐标系．则D（1,0,0），A（1,1,0），B（0,1,0），E（0,0,1），

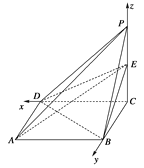
从而＝（0,1,0），＝（－1,0,1），＝（1,0,0），＝（0，－1,1）．[Z#x设平面ADE和平面ABE的法向量分别为，

由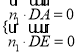，取

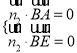
由，取

设二面角D－AE－B的平面角为θ，则，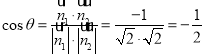

∴θ＝，即二面角D－AE－B的大小为